「場合の数や確率が苦手」
「場合の数の総復習がしたい」
今回は場合の数と確率に関する悩みを解決します。
場合の数と確率に関するまとめ記事を書きました。
本記事では、数学ⅠAの場合の数と確率について徹底解説します。
長い記事なので苦手な単元を選んで復習に使ってください。
場合の数と確率
数学を中心としたオンライン家庭教師「スタディトレーナー」生徒募集中！
個別指導のこれ以上ないサポートであなたを支えます。
場合の数
場合の数とは、ある事柄の起こりうる場合の総数を指します。
- サイコロの目の出方は何通りありますか？
- トランプの組み合わせは何通りありますか？
このように「全部で何通り？」を考えるのが場合の数です。
2つの事象によっては同時に起こらないこともあります。
例えば、サイコロを1回だけ投げて「1の目が出る事象」と「6の目が出る事象」は同時に起きません。
このとき、「この事象は互いに排反である」といいます。
和集合と積集合については以下の記事で詳しく解説します。
⇒場合の数~和の法則・積の法則~
-
場合の数を数えるには？和の法則と積の法則について解説！《場合の数》
続きを見る
順列
順列とは「異なるn個のものから異なるr個を取り出して並べること」を表します。
順列の総数
\(_{n}P_{r}=n(n-1)(n-2).....(n-r+1)\)
順列の公式の使い方を解説しました。
⇒順列Pの公式と使い方を5分でサクッと解説！
-
順列Pの公式と使い方を徹底解説！5分で分かる順列のコツ！
続きを見る
隣り合う順列
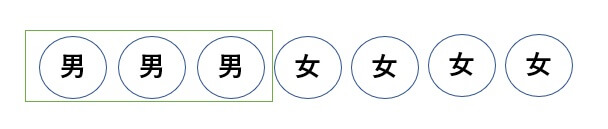
これは隣り合うときの問題なので、男子3人を１つの塊とみなしましょう。
するとこの問題は、男子の塊1つと女子4人の順列の問題として考えます。
男子の塊と女子4人の並び方の総数は、
\(5!=5・4・3・2・1=120\)通り
これだけではなく、男子の並び替えも考える必要があります。
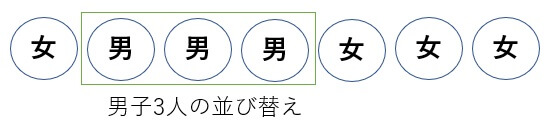
男子の塊の中でも並び替えがあるので
\(3!=3・2・1=6\)通り
したがって、男子3人が隣り合う並び方は
\(120\times{6}=720\)
答え 720通り
隣り合わない順列
次は隣り合わない問題なので、女子を並びたあとに両端および間に男子を入れていきます。
まず女子を並び替えます。
\(4!=4・3・2・1=24\)通り
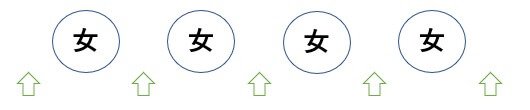
つぎの男子3人を入れる箇所を選びます。
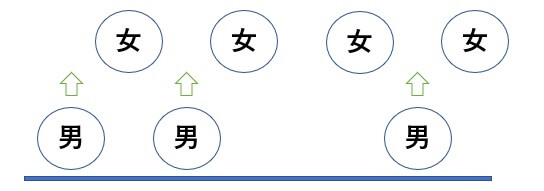
入れる男子の順番を決めます。
\(3!=3・2・1=6\)通り
よって男子が隣り合わない時の並び方の総数は
\(24\times{10}\times{6}=1440\)
答え 1440通り
隣り合う順列？隣り合わない順列？ 続きを見る
⇒隣り合う順列と隣り合わない順列の解き方のポイント！
隣り合う順列と隣り合わない順列の解き方のポイント！！
円順列
列ではなく円形に並んだ順列を円順列といいます。
両親2人と子供3人（たかし、あきら、ゆうき）の5人が円形のテーブルに座っています。
このとき5人全体の座り方は何通りありますか。
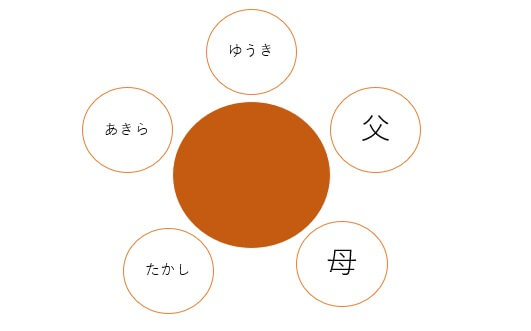
円順列はどこか1か所を固定することで順列と同じように考えることができます。
異なるn個のものを取り出し、円形に並べるときの並べ方の総数
-
円順列の公式と求め方を分かりやすく解説！なぜ円順列は1引くの？
続きを見る
重複順列
重複順列とは、「重複が許された順列」を指します。
重複が許されたというのは、同じものを何回も使ってよいということです。
この問題は重複が許されており、「111」や「121」など同じ数を何度も使うことができるので重複順列の問題です。
\(n\)個から\(r\)個取る重複順列
-
重複順列とは？重複順列の公式と使い方
続きを見る
組み合わせ
組み合わせとは、「異なる\(n\)個のものから異なる\(r\)個を取り出した1組」を指します。
順列は並び方を見ていたので順番が重要でしたが、組み合わせの場合は(A,B,C)と(B,C,A)は同じものとして考えます。
組み合わせの公式
\(\displaystyle _{n}C_{r}=\frac{n(n-1)(n-2)......(n-r+1)}{r(r-1)(r-2).....1}\)
-
組み合わせCの公式と使い方を徹底解説！5分でサクッと解説！
続きを見る
順列の問題と組み合わせの問題は見た目が似ているので注意が必要です。
しかし、次の２つを押さえておけば、ほとんどの問題は見分けられます。
順列と組み合わせの見分け方
- "並べる"ときは順列、"選ぶ"ときは組み合わせ
- 順番を気にしないときは組み合わせ
順列と組み合わせの見分け方はこちら
-
順列Pと組み合わせCの違いと"簡単"な見分け方
続きを見る
確率
場合の数が求められると、その事象が起きる確率を求めることができます。
たとえば、赤玉3個と青玉4個が入っている箱の中から、玉を1つ取り出します。
このとき取り出した玉が青玉の確率は7個の玉の中で青玉が4個入っているので
\(\displaystyle \frac{4}{7}\)
となります。
条件付き確率
-
条件付き確率の公式と求め方を分かりやすく解説！
場合の数と確率 まとめ
今回は場合の数と確率についてまとめました。
すこしでも誰かに役に立てていたら幸いです。
教科書に内容に沿った解説記事を挙げていくので、お気に入り登録して定期試験前に確認してください。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように！
定期テストにおすすめな映像授業
河合塾One
基本から学びたい方には河合塾Oneがおすすめ！
AIが正答率を判断して、あなただけのオリジナルカリキュラムを作成してくれます！
まずは7日間の無料体験から始めましょう！
スタディサプリ
会員数157万人の業界No.1の映像授業サービス。
月額2,178円で各教科のプロによる授業が受け放題！分からないところだけ学べるので、学習効率も大幅にUP！
本気で変わりたいならすぐに始めよう！
要チェック！
「どうして勉強したのに点数が下がるの...」
勉強しているのに成績が上がらない方は「【体験談】偏差値40から60まで上げたぼくの勉強法」を必見！
-
【やれば上がるはウソ】偏差値40から60まで上げたぼくの勉強法！
