「円順列の公式が知りたい」
「公式の意味が知りたい」
今回は円順列に関するこんな悩みを解決します。

今回は順列のなかでも円順列について解説します。
さっそくですが以下の問題をご覧ください。
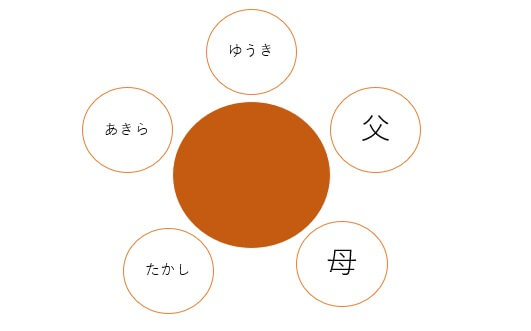
円順列 例題
両親2人と子供3人(たかし、あきら、ゆうき)が円形のテーブルに座っています。
このとき5人全体の座り方は何通りありますか。
これが円順列の問題です。
結論からいうと、この問題は
\[\left(5-1\right)!=24\]
となり、24通りだと求めることができます。
本記事では円順列の公式と意味について解説しています。
後半では円順列の問題解説をしているので、ぜひ最後までご覧ください。
記事の内容
いまなら公式LINEから簡単なアンケートに答えるだけで、『場合の数と確率』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください!

円順列の公式
円順列とは名前の通り円の順列を指します。
円順列の公式は以下のようになっています。
円順列の公式
異なる\(n\)個のものを円形に並べるときの並べ方の総数
\[\left(n-1\right)!\]
人が円形テーブルに座る問題や、輪の形に並ぶ問題が多いですね。
円順列と順列の違い
円順列と順列の違いは並べ方の違いです。
順列は1列にまっすぐ並べていくのに対して、円順列は円状に並べます。
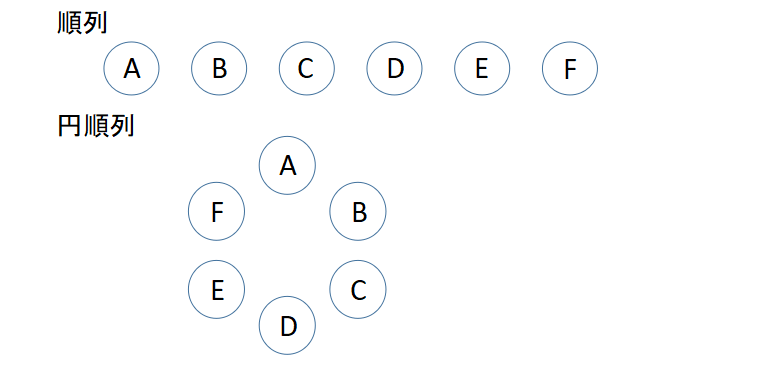
ただし、全ての順列の問題が1列に並べるとは限らないので、あくまでイメージとして理解しておくのが良いでしょう。

いまなら公式LINEから簡単なアンケートに答えるだけで、『場合の数と確率』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください!

円順列の公式の意味
ただの順列では、異なるn個のものを並べるときの並べ方は\(n!\)でしたね。
それに対して、円順列では
\[(n-1)!\]
となっています。


両親二人と子供3人(たかし、あきら、ゆうき)が円形のテーブルに座ったとします。
その中の1つの並び方として、以下の座り方があります。
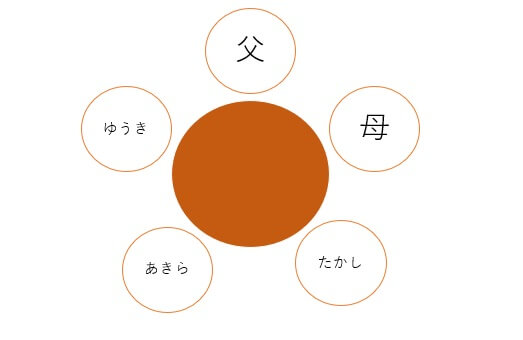
次にこちらをご覧ください。

実はこの2つの座り方は、見る向きを変えただけでどちらも同じ並び方です。
他にも同じ並び方となる例を見てみましょう。
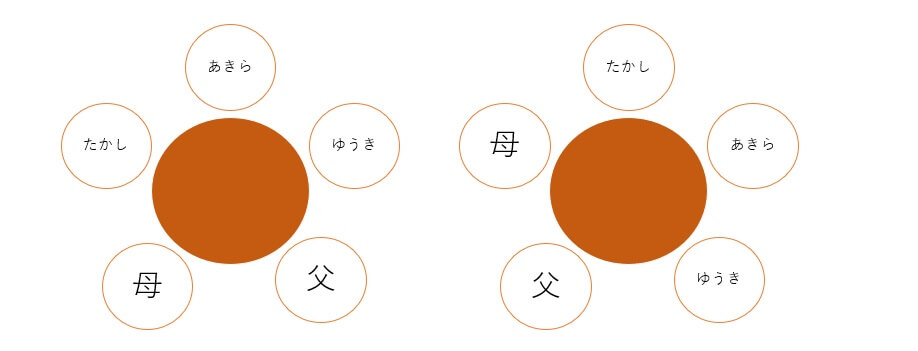
つまり、円順列を順列と同じく\(5!\)としてしまうと同じ座り方を何度も数えてしまいます。
そこでひと工夫したのが円順列の公式です。
円順列を考えるときは基準となるものを1つ決めましょう。
今回は例としてあきらさんを基準とします。
あきらさんを先頭にした順列を考え、そのまま円形に座ることで座り方の重複がなくなります。

したがって、今回の問題では基準としたあきらさんを除く4人の順列になります。
\[\left(5-1\right)!=24\]
よって、5人で円形テーブルに座るときの座り方は24通りになります。
例題のように、円順列では1つを基準として残りの順列を考えるので、以下のような公式になるのです。
円順列の公式
異なる\(n\)個のものを円形に並べるときの並べ方の総数
\[\left(n-1\right)!\]

円順列の問題
円順列は、円形テーブルの問題が非常に多いです。
円順列の問題
円形テーブルの問題のなかでも、
- 大人と子どもで座る問題
- 交互に座る問題
- 隣り合う問題 など
様々な問題があり難しそうに見えますが、意外とそんなことはありません。
考え方は順列のときと似ています。
テーブルを囲む問題
テーブルを囲む問題
5人で円形テーブルに座るとき、座り方は何通りありますか?
これは超基本となる円順列の問題です。
\begin{eqnarray}
(5-1)!&=&4!\\
&=&24
\end{eqnarray}
したがって、24通りだと分かりました。


交互に座る問題
交互に座る問題
大人5人と子ども5人が輪の形に並ぶとき、大人と子どもが交互に並ぶ並び方は何通りありますか?
これは先に大人を輪の形に並べたあとに、すき間に子どもを並べると考えましょう。
まずは大人を円状に並ばせるので、
\[(5-1)!=24\]
次に子どもを大人のすき間に並べます。
子どもを1列に並べて、すき間に入れていくので順列の考え方です。
\[5!=120\]
したがって、求める並び方は
\[24 \times 120 =2880\]
よって、2880通りだと分かりました。
隣り合う問題
隣り合わない
男子4人と女子2人が、6人の丸いテーブルに座ります。女子が隣り合う並び方は何通りありますか?
隣り合う問題と隣り合わない問題は順列でもありましたね。

隣り合う問題では、隣り合うものを1セットにして考えます。
つまり、今回の問題では女子2人を1セットで考えましょう。
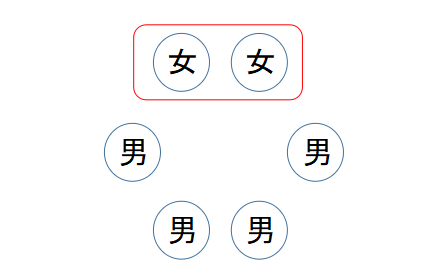
すると、女子1セットと男子4人の円順列になります。
\[(5-1)!=24\]
また、女子2人の並び替えもあるので、
\[24 \times 2 =48\]
したがって、女子2人が隣り合う並び方は48通りあります。
《応用》数珠順列

円順列とあわせてじゅず順列についても知っておくと良いでしょう。
じゅず順列の公式
\(n\)個の異なるもので輪を作るときの並べ方の総数
\[\displaystyle \frac{\left(n-1\right)!}{2}\]
円順列の公式を2で割るとじゅず順列の公式になります。
では、どういった問題がじゅず順列なのか見ていきましょう。
じゅず順列の例題
色の異なるビーズ5つをすべて使って、ブレスレットをつくります。ブレスレットは全部で何通り作ることができますか。
これはじゅず順列の問題です。
考え方は円順列の問題と似ています。
まずは5つを円形に並べる問題なので、\((5-1)!\)通り

円順列の問題では、以下の2つの並べ方は異なるものですがブレスレットとなると話は別です。
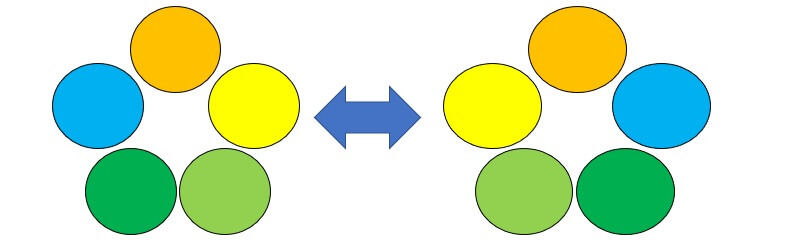
ブレスレットは裏返すことができるので、この2つは同じものとして扱います。
表と裏を考えた結果、ブレスレットは全部で\(\displaystyle \frac{(5-1)!}{2}\)通りあることが分かりました。
裏返したときに重複する並び方があるので、じゅず順列の公式は\(\displaystyle \frac{(n-1)!}{2}\)になるのです。
円順列《練習問題》

円順列を求める練習問題に挑戦してみましょう。

円順列の練習問題1
練習問題1
4人で円形のテーブルに座るとき、何通りの座り方がありますか。
解説
これは典型的な円順列の問題なので、円順列の公式に当てはめて考えましょう。
\begin{eqnarray}
(4-1)!&=&3!\\
&=&6
\end{eqnarray}
したがって、6通りだと分かりました。
円順列の練習問題2
練習問題2
大人2人と子ども4人が、円形のテーブルに座るとき、大人2人が向かい合う座り方は何通りありますか?
解説
大人のどちらかを基準とすると、シンプルに解くことができます。
大人1人を基準とすると、もう1人の大人の位置が決まります。
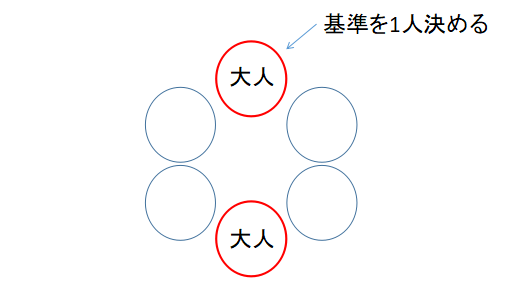
あとは子ども4人の順列を考えればよいので、
\[4!=24\]
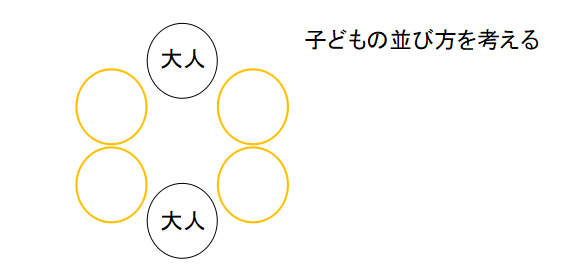
したがって、求めたい座り方は24通りあります。
円順列の公式 まとめ
今回は円順列の公式についてまとめました。
円順列 まとめ円順列は以下の公式で求めることができる。
円順列の公式
異なる\(n\)個のものを円形に並べるときの並べ方の総数
\[\left(n-1\right)!\]
円順列の考え方
円順列は基準となるものを決めることで、順列の問題として考えている。
今回は円順列の公式について解説しましたが、その他にも重要な公式はたくさんあります。
順列や組み合わせなど、場合の数の重要ポイントをまとめたのでぜひご覧ください。
-

場合の数と確率まとめ【完全攻略】
いまなら公式LINEから簡単なアンケートに答えるだけで、『場合の数と確率』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください!






