今回解決する悩み
「多項式がよく分からない」
「単項式と多項式の違いを知りたい」
今回は数Ⅰの「数と式」から、単項式と多項式についての悩みを解決していくよ！
こんにちは！数学講師のゆうやです！
高校生の勉強に関する相談に乗ったり、高校数学の解説記事を書いたりしています！
各種SNS情報
- マストラ公式LINE
⇒勉強に関する相談や質問がしたい - Instagram
⇒数学の公式や問題の解き方が知りたい - Twitter
⇒最新記事の情報をすぐにゲットしたい - オンライン指導スタディトレーナー
⇒個別指導で志望校合格を目指したい
さて、今回は単項式と多項式の違いについて考えていきましょう。
まずはこちらをご覧ください。
- 単項式
⇒\(x,3ab,-2x^{2}yz\) など - 多項式
⇒\(2x+3y,-ab+a-b\) など
どちらも数字と文字があるので、同じように見えていませんか？
ここが曖昧だとこの先ピンチなので、必ずそれぞれの意味と違いを理解しておきましょう。
本記事では、"単項式"と"多項式"の意味とその違いを解説しています。
単項式について知ろう
まずは単項式について確認していきましょう。
この機会に、単項式の意味と合わせて次数と係数の復習も入れておきました。
単項式の意味
単項式とは、「数や文字を掛けただけで作られる式」を指します。
単項式の例
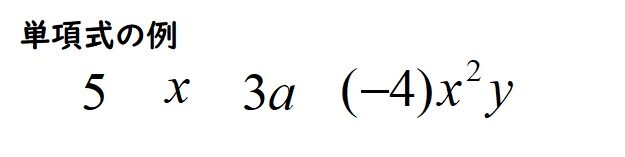
《単項式の例》
上図のような、数字と文字でできた塊が単項式です。
係数と次数
係数と次数についても復習しておきましょう。
単項式の数字の部分を、その単項式の係数といいます。
また、掛けた文字の個数のことを次数といいます。
メモ
\((-4)x^2y\)の場合は、係数が\(-4\)で文字は3個掛けられているので次数3となります。
\(1x\)は単に\(x\)と書いて、\((-4)x^2y\)は\(-4x^2y\)と書きます。
多項式について知ろう
次に多項式について解説していきます。
項が多いから"多項式"と考えるのが覚えやすくてオススメです。
多項式の意味
多項式とは、「単項式の和として表される式」です。
この説明だといまいちピンと来ないので、具体例をいくつか見てみましょう。
下の式はどれも多項式です。
多項式の例
\(2x+3y-5xy\)
\(-4x^{2}-3x+4\)
このような、単項式を2個以上含む、加法（足し算）の式を多項式といいます。
ここで、加法の式と言いつつも、マイナスがあることに疑問を抱いた方もいますよね。
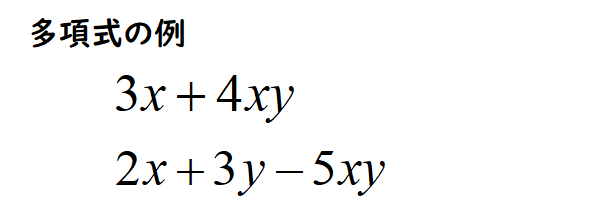
上の式は\(3x\)と\(4xy\)を項に持ち、ちゃんと加法の形になっているので多項式で納得できますね。
一方で、下の式は減法（引き算）を含んでいて、加法の形になっていないです。
ですが、実際は式の形を少し変えると、
\[2x+3y+(-5xy)\]
となります。
つまり、下の式も\(2x\),\(3y\),\((-5xy)\)の３つの項を持つ多項式です。
降べきの順に並べよう
降べきの順という言葉を聞いたことがありますか？
降べきの順に並べるとは、特定の文字の次数が下がっていく順に多項式の項を並び替えるということです。
以下のような多項式があったとしましょう。
\[5x-3x^{2}+2x^{3}+4\]
この多項式を\(x\)についての降べきの順に並べるとこのようになります。
\[2x^{3}-3x^{2}+5x+4\]
このように右に行くにつれて、\(x\)の次数が下がっていくような並べ方を降べきの順と言います。
高校で学習する関数のほとんどは降べきの順になっています。
また、次数が上がっていく順に並び替えることを"昇べきの順"ともいいます。
余裕があればこちらも覚えておきましょう。
参考
・昇べきの順
⇒右に行くにつれて次数が上がっていく
\[4+5x-3x^{2}+2x^{3}\]
単項式と多項式の違い
それでは、単項式と多項式の違いについて確認していきましょう。
結論から言うと、１つの項でできた式が単項式、2個以上の項でできた式が多項式です。
単項式と多項式の違い
式を作る項の数で見分けよう。
- 単項式
⇒項が１つ
例：\(x, 3abc, -4a^{2}b\) - 多項式
⇒2個以上の項
例：\(a+2, -3ab+2a-5b\)
もっと簡単に言うと、式が加法もしくは減法の形をしていればその式は多項式です
単項式と多項式《練習問題》
せっかく単項式と多項式の違いが理解できたので、練習問題に挑戦してもっと理解を深めよう！
練習問題①
次の単項式の係数と次数をいえ。
(1) \(7x^{2}\)
(2) \(-x^{2}y\)
(3) \(-5abc\)
解答
- 係数:7 次数:2
- 係数:-1 次数:3
- 係数:-5 次数:3
練習問題②
次の多項式を\(x\)について降べきの順になるよう整理せよ。
\[3x^{2}+x^{3}-14+2x\]
解答
\(x^{3}+3x^{2}+2x-14\)
定期テスト対策用の問題プリントを作成しています。
無料ダウンロードも可能、まとめて冊子で欲しい方は300円~販売中！
単項式と多項式 まとめ
今回は単項式と多項式の違いについて順を追って確認してきました。
意味さえ分かってしまえば、そこまで難しい話でもないのでこの機会で理解しておきましょう。
単項式と多項式の違い
式を作る項の数で見分けよう。
- 単項式
⇒項が１つ
例：\(x, 3abc, -4a^{2}b\) - 多項式
⇒2個以上の項
例：\(a+2, -3ab+2a-5b\)
１つの項でできた式が単項式、2個以上の項でできた式が多項式です。
整式を整理するときは、同類項をまとめることで多項式を見やすくします。
▼数学Ⅰ「数と式」の重要ポイントをまとめた記事を作りました。
-
数と式まとめ【完全攻略】
続きを見る
マストラ公式LINEアカウントを友達登録しよう！
マストラのLINE公式アカウントができました！
～実際の公式LINEのメニュー～
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ！
高校生向けの様々なコンテンツを配信予定！
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね！
▼この機会にぜひ登録！
完全個別指導のスタディトレーナー
スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服！
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応！
無料体験授業から始められるので、お気軽に申し込み下さい。
