「どれが実数か分からない」
「実数の具体例を教えて欲しい」
今回は実数に関するこんな悩みを解決します。
数学では、"実数"という言葉がよく出てきますね。
「なにが実数に含まれるんだっけ...」
高校生の僕もあまり分かっていませんでした。
結論から言うと、実数とは「有理数と無理数の総称」です。
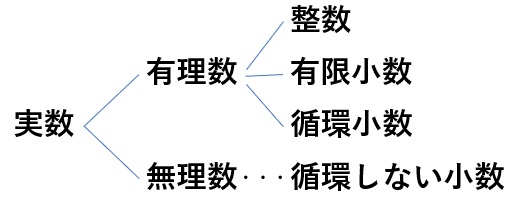
実数に含まれるもの
高校生数学の範囲で言うと、虚数以外はすべて実数です。
とても簡潔に結論だけを述べましたが、まだ完全な理解には至っていない方も多いでしょう。
本記事では実数の定義や具体例について解説しています。
実数でないものの例も紹介しているのでぜひ参考にしてください。
記事の内容
実数とは"有理数"と"無理数"の総称
まず、実数とは「有理数と無理数の総称」を表します。
高校数学で習う範囲で言うと、虚数以外の数はすべて実数に含まれます。
なので、分数やルート、πなども実数に含まれます。
実数の例
・整数
\[-3,-2,-1,0,1,2,3\]
・有限小数
\begin{eqnarray}
\displaystyle 0.125&=&\frac{1}{8}\\
\displaystyle 0.0001&=&\frac{1}{10000}
\end{eqnarray}
・循環小数
\begin{eqnarray}
\displaystyle 0.3333...&=&\frac{1}{3}\\
\displaystyle 0.2525...&=&\frac{25}{99}
\end{eqnarray}
・無理数(循環しない小数)
\begin{eqnarray}
\sqrt{2}=1.41421356...\\
\pi =3.14159265...
\end{eqnarray}
有理数と無理数の違い
実数は「有理数と無理数の総称」です。
ここで、「そもそも"有理数"と"無理数"って何？」という方もいますよね。
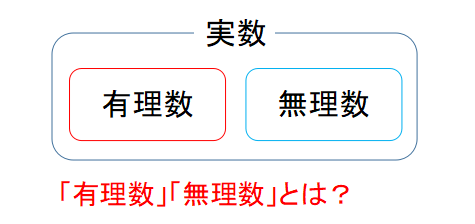
実数をバッチリと理解するために、有理数と無理数についても確認しましょう。
有理数とは？
有理数とは「分数の形で表せる数」を指します。
例としては以下のようなものがあります。
整数ならばどんな数でも分数にすることが可能ですね。
\[\displaystyle 3=\frac{3}{1},-2=-\frac{2}{1}\]
次に、0,5や0,125のような有限な小数を有限小数といいます。
有限小数は\(10^{n}\)を分母にすることで、分数で表すことができます。
有限小数\(\displaystyle =\frac{整数}{10^{n}}\)
\[\displaystyle 0.05=\frac{5}{100}\]
\[\displaystyle 0.1234=\frac{1234}{10000}\]
無限小数のなかでも、同じ数字を繰り返すものを循環小数といいました。
循環小数を分数に直すには、ひと手間加えます。
循環小数\(0.3333\cdots\)を例にすると、
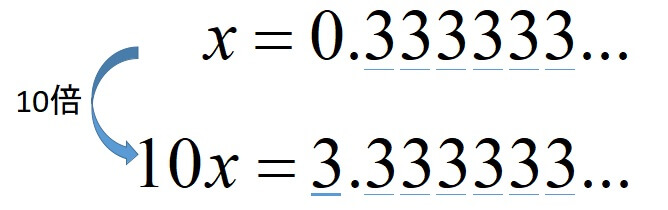
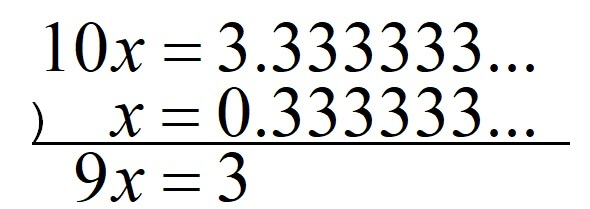
したがって、
\begin{eqnarray}
9x=3\\
\displaystyle x=\frac{1}{3}
\end{eqnarray}
循環小数を分数に直す方法は「循環小数の例と分数に直す方法」にて詳しく解説しています。
無理数とは？
一方で、「分数で表せない数」を無理数といいます。
無理数だと判断するのは簡単で、ルートや\(\pi\)などの循環しない小数が無理数です。
無理数とは？
無理数⇒循環しない小数
\(\sqrt{2},-\sqrt{5},\pi\)など
実数の例
有理数と無理数について解説しましたが、改めて実数の具体例を確認しましょう。
・整数
\[-3,-2,-1,0,1,2,3\]
・有限小数
\begin{eqnarray}
\displaystyle 0.125&=&\frac{1}{8}\\
\displaystyle 0.0001&=&\frac{1}{10000}
\end{eqnarray}
・循環小数
\begin{eqnarray}
\displaystyle 0.3333...&=&\frac{1}{3}\\
\displaystyle 0.2525...&=&\frac{25}{99}
\end{eqnarray}
・無理数(循環しない小数)
\begin{eqnarray}
\sqrt{2}=1.41421356...\\
\pi =3.14159265...
\end{eqnarray}
実数でないものの例
実数の具体例を確認しましたが、逆に実数でないものの例も確認しましょう。
実数でない数には、虚数や四次元数などが含まれます。
・虚数
\[2−5i,5+7i\]
・四次元数
\[a+bi+cj+dk\]
虚数とは複素数を表す数で、\(i^{2}=−1\)を満たす\(i\)を持つ数です。
複素数の例：\(2−5i,5+7i\)
四次元数とは複素数をさらに拡張したものです。
四次元数の一般項：\(a+bi+cj+dk\)（\(a,b,c,d\)は実数）
実数 まとめ
今回は実数の定義と具体例についてまとめました。
実数：有理数と無理数の総称
有理数：分数で表せる数
無理数：分数で表せない数
実数の例
・整数
\[-3,-2,-1,0,1,2,3\]
・有限小数
\begin{eqnarray}
\displaystyle 0.125&=&\frac{1}{8}\\
\displaystyle 0.0001&=&\frac{1}{10000}
\end{eqnarray}
・循環小数
\begin{eqnarray}
\displaystyle 0.3333...&=&\frac{1}{3}\\
\displaystyle 0.2525...&=&\frac{25}{99}
\end{eqnarray}
・無理数(循環しない小数)
\begin{eqnarray}
\sqrt{2}=1.41421356...\\
\pi =3.14159265...
\end{eqnarray}
実数はこれからもずっと使う言葉なので、必ず覚えておきましょう。
命題と条件について別の記事で解説しています。
-
命題とは？命題の意味と「逆・裏・対偶」の関係
-
必要条件・十分条件とは？違いと見分け方を分かりやすく解説！
それでは最後まで読んでくださりありがとうございました。
あなたの努力が報われますように！
マストラ公式LINEアカウントを友達登録しよう！
マストラのLINE公式アカウントができました！
～実際の公式LINEのメニュー～
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ！
高校生向けの様々なコンテンツを配信予定！
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね！
▼この機会にぜひ登録！
完全個別指導のスタディトレーナー
スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服！
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応！
無料体験授業から始められるので、お気軽に申し込み下さい。
![Pinterest](https://www.pinterest.com/pin/create/button/?url=https%3A%2F%2Fmath-travel.com%2Freal-number%2F&media=https://math-travel.com/wp-content/uploads/2020/12/実数とは.png&description=「どれが実数か分からない」 「実数の具体例を教えて欲しい」 今回は実数に関するこんな悩みを解決します。 高校生どれが実数なのかよく分かっていなくて... 数学では、"実数&qu){kind=link}