今回解決する悩み
「ルートのなかにルートがある」
「二重根号の外し方が知りたい」
今回は数Ⅰの「数と式」から、二重根号についての悩みを解決していくよ！
こんにちは！数学講師のゆうやです！
高校生の勉強に関する相談に乗ったり、高校数学の解説記事を書いたりしています！
各種SNS情報
- マストラ公式LINE
⇒勉強に関する相談や質問がしたい - Instagram
⇒数学の公式や問題の解き方が知りたい - Twitter
⇒最新記事の情報をすぐにゲットしたい - オンライン指導スタディトレーナー
⇒個別指導で志望校合格を目指したい
さて、今回は二重根号の外し方について考えていきましょう。
まずはこちらをご覧ください。
\[\sqrt{5+2\sqrt{6}}、\sqrt{5-2\sqrt{6}}\]
ルートの中にルートがあって、初めて見た人はビックリしますよね
二重根号は外し方は公式を知らないと、この後の計算に手も足も出ないです。
簡単な公式なので、この機会に必ず習得しておきましょう。
二重根号の外し方
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
本記事では、"二重根号"の外し方について解説していきます。
2がないパターンや、マイナスの二重根号についても解説してるのでぜひ最後までご覧ください。
二重根号とは？
今回解説する"二重根号"というのは、ルートのなかにルートがあるものを指します。
\[\sqrt{5+2\sqrt{6}}、\sqrt{5-2\sqrt{6}}\]
二重根号の解説をする前に、「根号」について確認しましょう。
根号というと難しいですが、ルート\(\sqrt{ }\)のことを指しています。
《根号の計算》
根号の計算
\[(\sqrt{5})^{2}=5\]
\[(-\sqrt{5})^{2}=5\]
\[-(\sqrt{5})^{2}=-5\]
根号の中身に文字が入っているときは、文字の符号によって場合分けが必要です。
二重根号の外し方
二重根号とは、ルートのなかにルートがあるものを指していました
\[\sqrt{5+2\sqrt{6}}、\sqrt{5-2\sqrt{6}}\]
このままでは計算が難しすぎますね。
以下の公式を使うことで、二重根号は2つのルートに形を変えることができます。
二重根号の外し方
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
公式だけ見せられてもピンと来ないですよね。実際に、二重根号を外してみましょう。
二重根号の外し方
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
まずは加法の形をした二重根号を外します。
この公式を思い出して、足して8、掛けて15になる数字の組み合わせを考えると、\(a=5,b=3\)の組がありますね。
よって、
\begin{eqnarray}
\sqrt{8+2\sqrt{15}}&=&\sqrt{(5+3)+2\sqrt{5\cdot 3}}\\
&=&\sqrt{5}+\sqrt{3}
\end{eqnarray}
これで二重根号を外すことができました。
同様の方法で、減法の形をした二重根号も外してみましょう。
二重根号の外し方
\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
この場合は、足して12、掛けて35になる数字の組み合わせを考えると、\(a=7,b=5\)の組がありますね。
よって、
\begin{eqnarray}
\sqrt{12-2\sqrt{35}}&=&\sqrt{(7+5)-2\sqrt{7 \cdot 5}}\\
&=&\sqrt{7}-\sqrt{5}
\end{eqnarray}
これで減法の二重根号も外すことができました。
二重根号の公式《証明》
二重根号の外し方の公式を証明しておきましょう。
なぜこの公式で二重根号を外すことができるのでしょうか。
二重根号の外し方
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
証明
二重根号の外し方を証明するには、以下の展開の公式がポイントになります。
ポイント
\[(a+b)^2=a^2+2ab+b^2\]
まずは加法の二重根号は、
\begin{eqnarray}
\sqrt{(a+b)+2\sqrt{ab}}&=&\sqrt{(\sqrt{a}+\sqrt{b})^{2}}\\
&=&|\sqrt{a}+\sqrt{b}|
\end{eqnarray}
となり、\(\sqrt{a}\)も\(\sqrt{b}\)も正の数なので
\[|\sqrt{a}+\sqrt{b}|=\sqrt{a}+\sqrt{b}\]
したがって、
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
減法の二重根号も同様の証明をします。
\begin{eqnarray}
\sqrt{(a+b)-2\sqrt{ab}}&=&\sqrt{(\sqrt{a}-\sqrt{b})^{2}}\\
&=&|\sqrt{a}-\sqrt{b}|
\end{eqnarray}
\(a>b>0\)ならば、\(\sqrt{a}-\sqrt{b}>0\)が成り立つので、
\[|\sqrt{a}-\sqrt{b}|=\sqrt{a}-\sqrt{b}\]
したがって、\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
2がない二重根号の外し方
二重根号の計算には以下のようなものもあります。
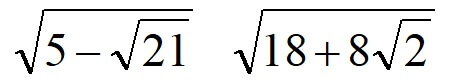
前半部分で紹介した二重根号とどこが異なるか分かりますか？
《2がない二重根号》
こういった二重根号を外すには工夫が必要です。
2を作るパターン
2を作るパターン
次の式を簡単にせよ。
\[\sqrt{4+\sqrt{15}}\]
二重根号は足してAの部分、掛けてBの部分になる、\(a,b\)の組み合わせを探します。
しかし、このままだとBの根号の前に２がないので無理やり式変形をします。
\begin{eqnarray}
\displaystyle \sqrt{4+\sqrt{15}}&=&\sqrt{\frac{8+2\sqrt{15}}{2}}\\
\displaystyle &=&\frac {\sqrt{8+2\sqrt{15}}}{\sqrt{2}}\\
\displaystyle &=&\frac {\sqrt{3}+\sqrt{5}}{\sqrt{2}}\\
\displaystyle &=&\frac {\sqrt{6}+\sqrt{10}}{2}
\end{eqnarray}
これで二重根号を外すことができました。
2になるように調整するパターン
2をなるように調整するパターン
次の式を簡単にせよ。
\[\sqrt{14-6\sqrt{5}}\]
根号の係数が6なので、2になるように調整します。
\[\sqrt{14-6\sqrt{5}}=\sqrt{14-2\sqrt{45}}\]
こうなってしまえば、二重根号の公式に当てはめて、
足して14、掛けて45になる数の組み合わせは、\((a,b)=(9,5)\)
\begin{eqnarray}
\sqrt{14-6\sqrt{5}}&=&\sqrt{14-2\sqrt{45}}\\
&=&\sqrt{9}-\sqrt{5}\\
&=&3-\sqrt{5}
\end{eqnarray}
よって、二重根号を外すことができました。
二重根号を外す《練習問題》
二重根号の式を簡単にする問題を解いてみましょう。
二重根号を外す
次の二重根号を簡単にしよう。
\((1) \sqrt{7+2\sqrt{10}}\)
\((2) \sqrt{5+\sqrt{21}}\)
\((3) \sqrt{18+8\sqrt{2}}\)
(1)の解説
これは二重根号の公式がそのまま使えるパターンですね。
\begin{eqnarray}
\sqrt{7+2\sqrt{10}}&=&\sqrt{(5+2)+2\sqrt{5 \cdot 2}}\\
&=&\sqrt{5}+\sqrt{2}
\end{eqnarray}
(2)の解説
これは2がないので工夫が必要です。
\begin{eqnarray}
\displaystyle \sqrt{5+\sqrt{21}}&=&\sqrt{\frac{10+2\sqrt{21}}{2}}\\
\displaystyle &=&\frac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}\\
\displaystyle &=&\frac{\sqrt{14}+\sqrt{6}}{2}
\end{eqnarray}
(3)の解説
これは2をつくる工夫が必要です。
\begin{eqnarray}
\displaystyle \sqrt{18+8\sqrt{2}}&=&\sqrt{18+2\sqrt{32}}\\
\displaystyle &=&\sqrt{16}+\sqrt{2}\\
\displaystyle &=&4+\sqrt{2}\\
\end{eqnarray}
二重根号の外し方 まとめ
今回は二重根号の外し方についてまとめました。
二重根号の外し方 まとめ
二重根号は以下の公式を使うと、簡単な形に変えることができます。
二重根号の外し方
\(a>0,b>0\)とすると
\[\sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}\]
\(a>b>0\)のとき
\[\sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\]
公式は簡単なのでたくさん問題を解き、公式に慣れていきましょう。
三乗の公式について知りたい方はこちらの記事がおすすめです。
-
【三乗の公式】(a±b)3乗の展開公式と覚え方を解説！
▼数学Ⅰ「数と式」の重要ポイントをまとめた記事を作りました。
-
数と式まとめ【完全攻略】
続きを見る
マストラ公式LINEアカウントを友達登録しよう！
マストラのLINE公式アカウントができました！
～実際の公式LINEのメニュー～
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ！
高校生専用のオンライン自習室など
様々なコンテンツを配信予定！
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね！
▼この機会にぜひ登録！
完全個別指導のスタディトレーナー
スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
9つのサポート
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- オンライン自習室も完備
- 進路相談もいつでも受付
- 1人じゃないから続けられる
- 苦手科目はプロ講師が1対1で指導
2022年度は定員8名としているので、ご希望の方は早めにお申し込みください。
