「分散ってなんだっけ?」
「分散の求め方が分からない」
今回はデータの分散に関する悩みを解説します。

分散に苦手意識を持つ学生はかなり多いですよね。
分散はデータの散らばりを表す指標の1つです。分散の値からデータの分布がイメージできます。
分散は偏差(データと平均値の差)を二乗したものの平均で求めることができます。
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\(\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\)
\(=\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}\)
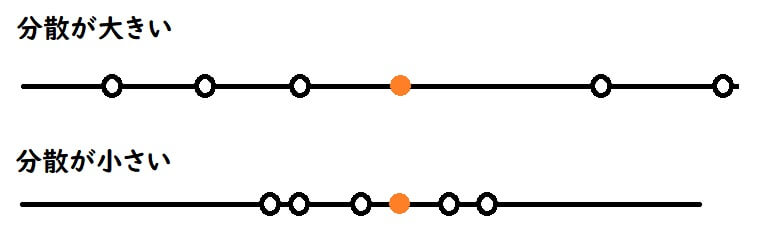
分散が大きいとデータの分布が広く、分散が小さいと同じようなデータが多いことが分かります。
データの分散は定期テストや共通テストでよく出題されます。
この機会に確実に押さえておきましょう。
本記事では、分散の公式と分散の求め方について解説しています。
分散が求められるようになると、標準偏差や相関係数を求められるようになります。
本記事の内容
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
分散とは?
分散とはデータの散らばりの度合いを表す指標です。
分散の大小によってデータ全体の分布をイメージすることができます。

分散の大小
分散が大きい⇒平均値から離れている値が多い
分散が小さい⇒平均値に近い値が多い
分散が大きいというのは、散らばりの度合いが大きいことを表します。
分散が分かるとデータ全体の分布がイメージしやすくなります。そのため分散はいろいろな研究で用いられる指標になっています。
分散の公式
分散を求める公式は2つあります。
分散の公式①
偏差(データと平均値の差)を二乗した平均が分散です。
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\(\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\)
\(=\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}\)
分散の公式②
分散は「2乗の平均」と「平均の2乗」の差でも求めることができます。
変数\(x\)の値を\(x_1,x_2,...,x_n\)、平均を\(\bar{x}\)とするとき
分散\(s^{2}\)は、
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)


いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。

分散の求め方
分散の公式を2つ紹介しました。
分散の公式①
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\(\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\)
\(=\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}\)
分散の公式②
変数\(x\)の値を\(x_1,x_2,...,x_n\)、平均を\(\bar{x}\)とするとき
分散\(s^{2}\)は、
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)
それぞれの公式を用いて分散を求める手順を解説します。
公式①で求める
分散の公式①
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\(\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\)
\(=\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}\)
分散を求め方①
- 平均値を求める
- 偏差(データと平均の差)を求める
- 偏差の二乗平均を求める
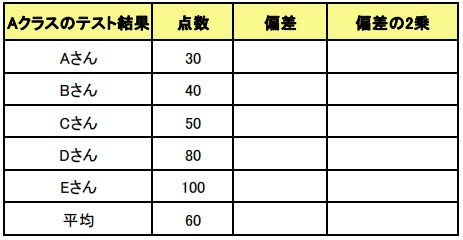
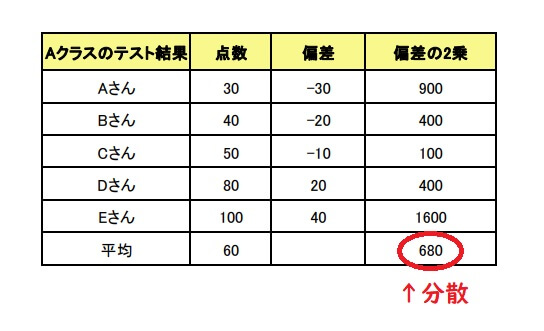
Aクラスのテスト結果の分散を求めましょう。
Aクラスのテスト結果
30 40 50 80 100 (点)
1.平均値を求める
まずは平均点\(\bar{x}\)を求めます。
\(\displaystyle \bar{x}=\frac{1}{6}(30+40+50+80+100)\)
\(=60\)
2.偏差を求める
偏差とは、データの値と平均の差を指します。
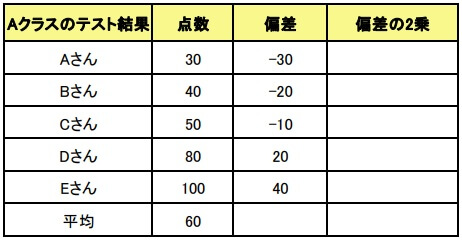
偏差を求める
\(30-60=-30\)
\(40-60=-20\)
\(50-60=-10\)
\(80-60=20\)
\(100-60=40\)
偏差については「偏差値の意味と求め方」にて詳しく解説しています。
3.偏差の二乗平均を求める
最後に偏差の二乗平均を求めます。
\(\displaystyle \frac{1}{5}\{(-30)^{2}+(-20)^{2}+(-10)^{2}+20^{2}+40^{2}\}\)
\(=680\)
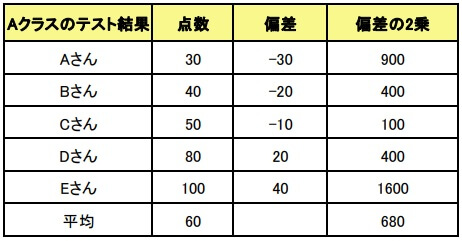
したがって、分散は680です。
公式②で求める
分散の公式②
変数\(x\)の値を\(x_1,x_2,...,x_n\)、平均を\(\bar{x}\)とするとき
分散\(s^{2}\)は、
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)
分散を求め方②
- データの2乗平均を求める
- 平均値の2乗を求める
- 分散を求める
先程の分散をこちらの方法でも計算してみます。
Aクラスのテスト結果
30 40 50 80 100 (点)
1.データの2乗平均を求める
まずはデータの2乗の平均を求めます。
テストの点数は30,40,50,80,100なので、
\(\displaystyle \frac{30^{2}+40^{2}+50^{2}+80^{2}+100^{2}}{5}\)
\(=\displaystyle \frac{900+1600+2500+6400+10000}{5}\)
\(=\displaystyle \frac{21400}{5}\)
\(=4280\)
これで2乗の平均は4280だと分かりました。
2.平均値の2乗を求める
つぎにテストの平均点の2乗を求めます。
Aクラスの平均点は60点なので、
\(60^{2}=3600\)
3.分散を求める
変数\(x\)の値を\(x_1,x_2,...,x_n\)、平均を\(\bar{x}\)とするとき
分散\(s^{2}\)は、
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)
分散\(s^{2}\)={2乗の平均}-{平均の2乗}
\(=4280-3600\)
\(=680\)
したがって、分散は680だと分かりました。
これは分散の公式①で求めた分散と同じになりました。
ココに注意
分散を求めるときは、与えられている情報を参考にどちらの公式を使うか判断してください。
おすすめ記事
分散の公式の証明
分散の公式について証明します。
公式①は分散の定義なので、そういうものだと理解してください。
ここでは分散の公式②について証明していきます。
変数\(x\)の値を\(x_1,x_2,...,x_n\)、平均を\(\bar{x}\)とするとき
分散\(s^{2}\)は、
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)
\(\displaystyle s^{2}=\frac{1}{n} \sum_{i=1}^n (x_{i}-\bar{x})^{2}\)
\(\displaystyle =\frac{1}{n} \sum_{i=1}^n (x_{i}^{2}-2x_{i} \bar{x} +\bar{x}^{2})\)
\(\displaystyle =\frac{1}{n} \sum_{i=1}^n (x_{i}^{2}-2x_{i} \bar{x} +\bar{x}^{2})\)
\(\displaystyle =\frac{1}{n} \sum_{i=1}^{n} x_{i}^{2}-2 \bar{x} \underbrace{\frac{1}{n} \sum_{i=1}^{n} x_{i}}_{=\bar{x}}+\frac{1}{n} \cdot n \bar{x}^{2}\)
\(\displaystyle =\frac{1}{n} \sum_{i=1}^{n} x_{i}^{2}-2 \bar{x}^{2}+\bar{x}^{2}\)
\(\displaystyle =\frac{1}{n} \sum_{i=1}^{n} x_{i}^{2}-\bar{x}^{2}\)
分散と標準偏差
分散の正の平方根を標準偏差といいます。

標準偏差が分かるとデータが分布する範囲が分かります。
なぜならば、標準偏差はほとんどのデータが「平均値±標準偏差」の範囲に収まっていることを表すからです。
参考
テストの結果が平均点60点、標準偏差20点のとき
テスト結果のほとんどが40点から80点のあいだに収まっていることを表します。
共分散との違い
分散と似た言葉で共分散というものがあります。
\(\displaystyle s_{x y}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)\)
分散が1つのデータの散らばりを表すのに対して、共分散は「2組の対応するデータの間にある関係」を表します。

共分散については「共分散の意味と求め方」で詳しく解説しています。
-

共分散の公式と求め方を2つ解説!図を使って考えてみよう!
続きを見る
分散《練習問題》

ここまで分散の公式や求め方について解説してきました。
最後に分散を使った練習問題に挑戦してみましょう。
練習問題Cクラスの国語のテスト結果の分散を求めよ。
テスト結果 40,50,60,60,90
分散の求め方①
分散の求め方①
- 平均値を求める
- 偏差(データと平均の差)を求める
- 偏差の二乗平均を求める
\(\displaystyle \frac{1}{5}(40+50+60+60+90)\)
\(=60\)
Cクラスの平均点は60点です。
それぞれの偏差を求めます。
\(40-60=-20\)
\(50-60=-10\)
\(60-60=0\)
\(60-60=0\)
\(90-60=30\)
最後に偏差を2乗して分散を求めます。
\(\displaystyle \frac{1}{5}\{(-20)^{2}+(-10)^{2}+0+0+30^{2}\}\)
\(=280\)
したがって、求める分散は280である。
分散の求め方②
分散の求め方②
- データの2乗平均を求める
- 平均値の2乗を求める
- 分散を求める
2乗の平均を求めます。
\(\displaystyle \frac{40^{2}+50^{2}+60^{2}+60^{2}+90^{2}}{5}\)
\(=\displaystyle \frac{19400}{5}\)
\(=3880\)
次に平均の2乗を求めます。
Cクラスの平均点は60点なので、
\(60^{2}=3600\)
分散\(s^{2}=3880-3600=280\)
したがって、求める分散は280である。
どちらも同じ数字になったので間違いはなさそうです。
データの分散 まとめ
今回はデータの分散についてまとめました。
公式は複雑ですが慣れればスムーズに求めることができます。
データの分散 まとめ
分散はデータの散らばりを表す指標で、分散の値からデータ全体の分布がイメージできる。
分散の公式
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\(\displaystyle \frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\)
\(=\displaystyle \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}\)
もしくは
\(\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\)

分散の大小
分散が大きい⇒平均値から離れている値が多い
分散が小さい⇒平均値に近い値が多い
分散が求められると標準偏差や相関係数を求めることができます。
標準偏差や相関係数もテストで出題されるので確認しておきましょう。
-

標準偏差の公式と求め方を徹底解説します!
続きを見る
-

相関係数の意味と求め方を分かりやすく解説!
続きを見る
[
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。











