数学Ⅰデータの分析で多くの高校生を悩ませるのが『共分散』です。
今回解決する悩み
「共分散の公式が知りたい」
「共分散の求め方が分からない」
今回はデータの中でも共分散に関するこんな悩みを解決します。
共分散とは「2組の対応するデータ間の関係を表す数値」です。
共分散の公式
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n (x_i -\overline{x})(y_i -\overline{y})\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
本記事では、共分散の意味や求め方について解説します。
分散が分かればすぐ理解できるのでしっかり理解しておきましょう！
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
共分散とは？
共分散とは「2組の対応するデータ間の関係を表す数値」です。
⇒共分散を求めることで「２つのデータの関係性」を分析することができます。
共分散と似たもので「分散」というものがありましたが覚えていますか？
分散は１つのデータの散らばり度合いを表しますが、今回の「共分散」は2つのデータの関係を表します。
分散については別の記事で解説しています。
もっと詳しく
分散の求め方について解説しました
共分散の求め方
では共分散の求め方について解説していきますが、共分散には2つの求め方があります。
スムーズに共分散を求めるには、どちらの公式も頭に入れておく必要があります。
共分散の公式①
共分散は「xの偏差×yの偏差」の平均で求めることができます。
偏差とは「データ値と平均値との差」を指します。
⇒詳しくは「偏差値の意味と求め方」で解説しています。
共分散の公式①
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n (x_i -\overline{x})(y_i -\overline{y})\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
文字では分かりづらいと思うので、具体例を見てみましょう。
共分散の例題
高校生5人が数学と英語のテストを受けました。
\(x\) :数学の点数 , \(y\) :英語の点数
5人の結果は以下のようになりました。
\((x,y)=(40,50)(50,60)(60,80)\)
\((70,60)(80,100)\)
この時の共分散を求めましょう。
与えられた情報を表にまとめました。
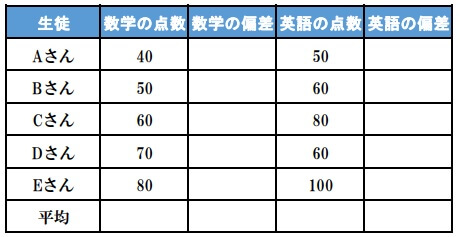
分散を求めるまでに3つのステップがあります。
共分散の求め方①
- \(x, y\)の平均値を求める
- それぞれの偏差を求める
- 偏差の積の平均値を求める
step
1\(x, y\)の平均値を求める
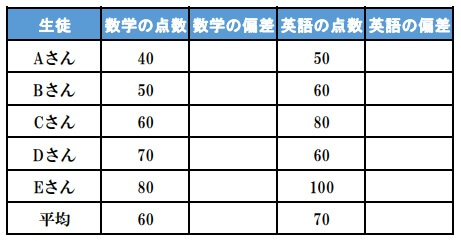
まずはそれぞれの平均値を求めましょう。
\(x, y\)の平均値を求めたものが以下の表です。
平均値の求め方はこちら 続きを見る
平均値の求め方を解説！中央値との違いはズバリこれ！
step
2それぞれの偏差を求める
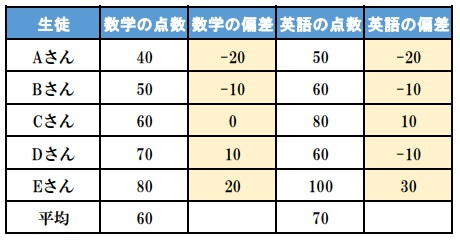
平均値が求められたら、それぞれの偏差を求めます。
偏差の計算
偏差＝（データ値）ー（平均値）
step
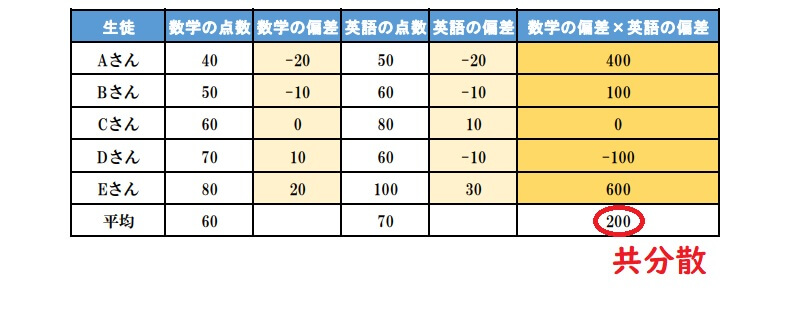
3偏差の積の平均値を求める
最後にそれぞれの偏差を掛け合わせた平均を求めるとそれが共分散です。
共分散の公式②
共分散を求める公式はもう1つあります。
共分散の公式②
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n x_i y_i - \overline{x} \overline{y}\]
すなわち
\[\displaystyle s_{xy}=\overline{xy}- \overline{x} \overline{y}\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
こちらの公式でも分散を求めてみましょう。
共分散の例題
高校生5人が数学と英語のテストを受けました。
\(x\) :数学の点数 , \(y\) :英語の点数
5人の結果は以下のようになりました。
\((x,y)=(40,50)(50,60)(60,80)\)
\((70,60)(80,100)\)
この時の共分散を求めましょう。
与えられた情報から表を作りました。
こちらの公式でも3つのステップがあります。
共分散の求め方②
- \(x, y\)の平均値\(\overline{x}, \overline{y}\)を求める
- \(xy\)の平均値\(\overline{xy}\)と\(\overline{x} \overline{y}\)を求める
- \(\overline{xy}\)と\(\overline{x} \overline{y}\)の差を求める
step
1\(x, y\)の平均値\(\overline{x}, \overline{y}\)を求める
5人の点数を元に数学と英語の平均値を求めます。
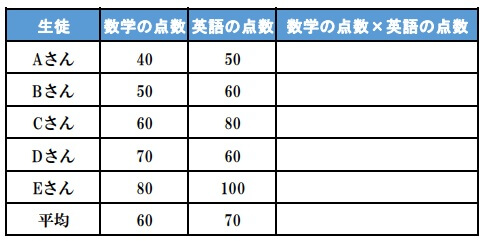
\(\overline{x}=60 , \overline{y}=70\)だと分かりました。
平均値の求め方が分からない人は「平均値の求め方を解説！」をご覧ください。
step
2\(xy\)の平均値\(\overline{xy}\)と\(\overline{x} \overline{y}\)を求める
\begin{eqnarray}
\displaystyle \overline{xy}&=&\frac{2000+3000+4800+4200+8000}{5}\\
&=&4400
\end{eqnarray}
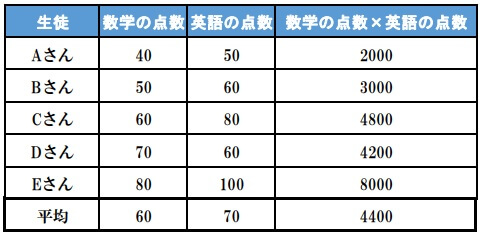そして\(\overline{x} \overline{y}\)も求めます。
\[\overline{x} \overline{y}=60 \cdot 70 =4200\]
step
3\(\overline{xy}\)と\(\overline{x} \overline{y}\)の差を求める
最後に\(\overline{xy}\)と\(\overline{x} \overline{y}\)の差を求めます。
\begin{eqnarray}
\displaystyle s_{xy}&=&\frac{1}{n} \sum_{i=0}^n x_i y_i - \overline{xy}\\
&=&\overline{xy}-\overline{x} \overline{y}\\
&=&4400 -4200\\
&=&200
\end{eqnarray}
となり、共分散は200と求めることができました。
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
共分散の値と符号の意味
共分散の値が何を意味するのか解説します。
共分散の符号
共分散が0⇒xとyの間に関係が見られない
共分散の値が小さい⇒xが大きい時、yは小さい
共分散の符号が正の時は相関の関係で、負の時は逆相関の関係が見られることを意味します。
共分散を表す記号
共分散は英語で「Covariance」というので、xとyの共分散をCov(x,y)と書きます。
また、\(σ_{xy}\)と書くこともあります。
共分散は「xの偏差×yの偏差」の平均でした。
平均値（期待値）を意味するEを用いて、
\(E[(x-\overline{x})(y-\overline{y})]\)
と表すこともあります。
共分散の注意点
共分散の注意点としては、扱っているデータの値が大きいと共分散の値も大きくなる点です。
共分散の値が大きいからといって２つのデータ間に強い相関の関係があるとは限りません。
⇒共分散 200(x,y)=(400,500)(500,600)(600,800)(700,600)(800,1000)
⇒共分散 20000
この注意点を解決してくれるのが相関係数です。
相関係数については「相関係数の意味と求め方」でまとめています。
-
相関係数の意味と求め方を分かりやすく解説！
続きを見る
共分散＜練習問題＞
共分散を使った練習問題に挑戦してみましょう。
共分散の練習問題
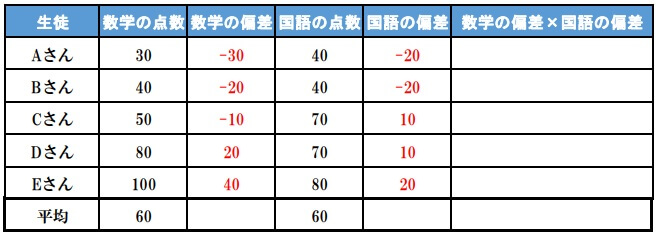
あるクラスで数学と国語のテストを行いました。
\(x\) :数学の点数 \(y\) :国語の点数
\[(x,y)=(30,40)(40,40)(50,70)\)
\((80,70)(100,80)\)
この共分散を求めよう。
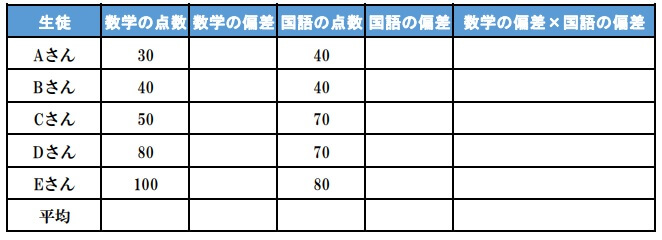
では、共分散の練習問題に取り掛かっていきます。
簡単な流れ
- \(x, y\)の平均値を求める
- それぞれの偏差を求める
- 偏差の積の平均値を求める
1.x,yの平均値を求める
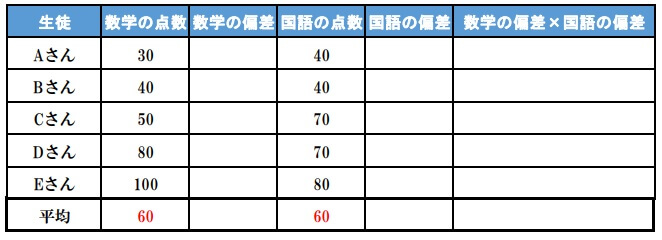
2.それぞれの偏差を求める
3.偏差の積の平均値を求める
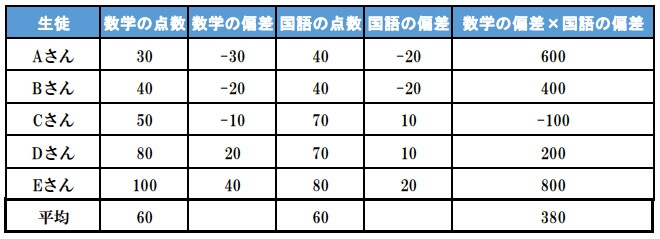
したがって、求める共分散は380である。
共分散の求め方 まとめ
今回は数Ⅰデータの分析のなかでも「共分散」について解説しました。
共分散のポイント
🔵共分散の公式①
共分散の公式①
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n (x_i -\overline{x})(y_i -\overline{y})\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
🔵共分散の公式②
共分散の公式②
\(x\)と\(y\)の共分散\(s_{xy}\)は次の公式で求める
\[\displaystyle s_{xy}=\frac{1}{n} \sum_{i=0}^n x_i y_i - \overline{x} \overline{y}\]
すなわち
\[\displaystyle s_{xy}=\overline{xy}- \overline{x} \overline{y}\]
nはデータの総数
\(x_i\)と\(y_i\)は個々の数値
\(\overline{x}\)と\(\overline{y}\)はそれぞれの平均値
共分散は「データの分析」のなかでも難しいほうです。
まずは解き方を覚えられるように問題集で繰り返し練習しましょう。
データの分析には重要な公式がたくさんあります。
分散や相関係数についても別記事でまとめているので合わせてご覧ください。
他にもデータの分析に関する悩みがある方は「データの分析まとめ記事」をご覧ください。
-
【数学Ⅰ】データの分析重要公式まとめ《完全攻略》
続きを見る
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
