「標準偏差は何を表してるの？」
「標準偏差の求め方は？」
今回は標準偏差に関する悩みを解決します。
標準偏差とは、「データの散らばりの度合い」を表す指標の1つです。
分散の正の平方根が標準偏差です。
本記事では、標準偏差の意味と求め方について解説します。
記事の内容
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
標準偏差の公式
標準偏差とは「データの散らばりの度合いを表す指標」の1つです。
分散の平方根で求めることができます。
分散の公式
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\begin{eqnarray}
\displaystyle s^{2}&=&\frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\\
\displaystyle &=&\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}
\end{eqnarray}
もしくは
\[\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\]
標準偏差\(s\)は分散\(s^{2}\)の正の平方根
\[s=\sqrt{s^{2}}\]
分散については「分散とは？分散の意味と求め方」にて解説しています。
-
分散とは？分散の公式と求め方を解説！標準偏差や共分散との違いは？
続きを見る
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
標準偏差の求め方
標準偏差\(s \)は分散\(s^2\) を使って以下のように表されます。
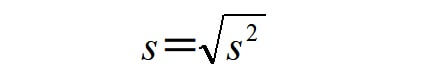
標準偏差は「分散の正の平方根」なので、まずは分散を求める必要があります。
標準偏差の求め方
- 平均値を求める
- 偏差を求める
- 分散（偏差の2乗平均）を求める
- 分散の平方根を求める
それでは、例をもとに一緒に標準偏差を求めてみましょう。
あるクラスで数学Ⅰのテストを行いました。
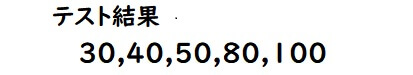
1.平均値を求める
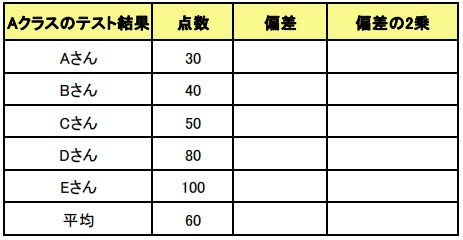
まずは平均値を求めます。
\[\displaystyle \frac{30+40+50+80+100}{5}=60\]
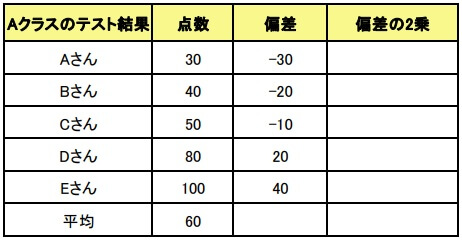
2.偏差を求める
偏差とは「データと平均値との差」を指します。
偏差を求める
偏差＝（データ値）-（平均値）
\begin{eqnarray}
30-60&=&-30\\
40-60&=&-20\\
50-60&=&-10\\
80-60&=&20\\
100-60&=&40
\end{eqnarray}
偏差について別の記事でまとめました。 続きを見る
偏差値とは？偏差値の意味と求め方をズバリ解説します！
偏差値とは？偏差値の意味と求め方をズバリ解説します！
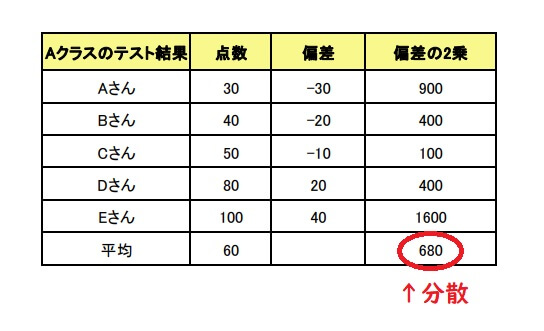
3.分散を求める
分散は「偏差の2乗平均」で求めることができます。
\[\displaystyle \frac{900+400+100+400+1600}{5}=680\]
分散の意味や求め方は別の記事で詳しくまとめています。
-
分散とは？分散の公式と求め方を解説！標準偏差や共分散との違いは？
続きを見る
4.分散の平方根を求める
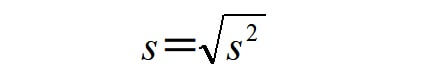
分散:680の正の平方根を求めます。
\[\sqrt{680} ≒ 26.08\]
したがって、標準偏差は26.08
これで標準偏差を求めることができました。
標準偏差のメリット
標準偏差を求めるメリットは「データ全体のざっくりとした分布」が分かることです。
例えば、あるテスト結果の分散が680と言われてピンと来ますか？おそらく誰も分からないでしょう。
しかし、標準偏差が26.08だと分かると、受験者の68%が”平均点±26.08点"の中にいることを示します。
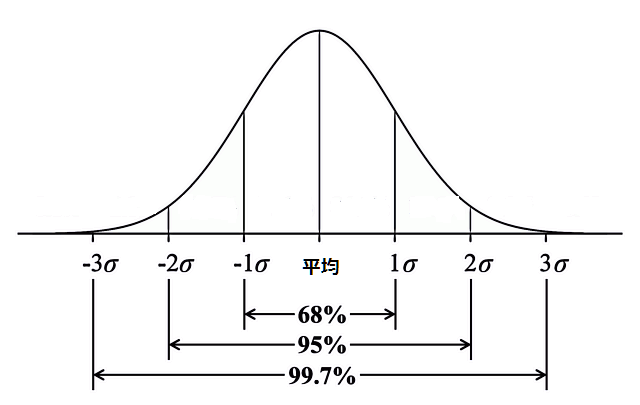
図のように、正規分布の場合、平均値±標準偏差中に観測データが含まれる確率は68.3%になります。
これが±標準偏差の２倍、３倍になるとさらに確率は上がります。
| 範囲 | 範囲内に収まる確率 |
|---|---|
| 平均値±標準偏差 | 68.3% |
| 平均値±（標準偏差×2） | 95.4% |
| 平均値±（標準偏差×3） | 99.7% |
標準偏差と分散
標準偏差と分散は何が違うのでしょうか。
ざっくりした説明ですが表している単位が異なるのです。
例えばお肉の重さについて調べます。このとき使う単位をグラム\(g\)だとしましょう。
分散はデータの2乗平均なので、求めた分散の単位は\(g^2\)になります。
その一方で、標準偏差は分散の正の平方根なので単位が\(g\)になっています。
したがって、データの散らばりの度合いを表すときは、分散の\(g^{2}\)よりも標準偏差で表した方が分かりやすくなります。
標準偏差を求めることで、ほとんどのデータが「平均値±標準偏差」に収まっていることが分かります。
標準偏差＜練習問題＞
標準偏差の意味を理解したところで、練習してみましょう。
先程のテストをBクラスでも行った結果、このようになりました。
Bクラスの標準偏差を求めましょう。
標準偏差の求め方を振り返ります。
標準偏差の求め方
- 平均値を求める
- 偏差を求める
- 分散（偏差の2乗平均）を求める
- 分散の平方根を求める
1.平均値を求める
\[\displaystyle \frac{40+55+60+70+75}{5}=60\]
平均値:60点
2.偏差を求める
\begin{eqnarray}
40-60&=&-20\\
55-60&=&-5\\
60-60&=&0\\
70-60&=&10\\
75-60&=&15
\end{eqnarray}
3.分散を求める
\begin{eqnarray}
\displaystyle s^{2}=\frac{(-20)^2+(-5)^2+0+10^2+15^2}{5}\\
\displaystyle &=&\frac{400+25+0+100+225}{5}\\
\displaystyle &=&\frac{750}{5}\\
&=&150
\end{eqnarray}
分散：150
4.分散の平方根を求める
分散が150なので、
\(\sqrt{150} ≒ 12.25\)
標準偏差 まとめ
今回はデータの分析から標準偏差についてまとめました。
標準偏差 まとめ標準偏差とは？
⇒データの散らばりの度合いを表す指標
分散の公式
変数\(x\)の値が\(x_1,x_2,...,x_n\)で、平均が\(\bar{x}\)のとき
分散\(s^{2}\)は、
\begin{eqnarray}
\displaystyle s^{2}&=&\frac{1}{n}\{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}\}\\
\displaystyle &=&\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^{2}
\end{eqnarray}
もしくは
\[\displaystyle s^{2}=\frac{1}{n}\sum_{i=1}^n x_i^{2} -\bar{x}^{2}\]
標準偏差\(s\)は分散\(s^{2}\)の正の平方根
\[s=\sqrt{s^{2}}\]
標準偏差は「分散の正の平方根」なので、まずは分散を求める必要があります。
標準偏差の求め方
- 平均値を求める
- 偏差を求める
- 分散（偏差の2乗平均）を求める
- 分散の平方根を求める
標準偏差に合わせて「共分散」や「相関係数」についても確認しておきましょう。
まだチェックしていない方はぜひご覧ください。
-
共分散の公式と求め方を2つ解説！図を使って考えてみよう！
続きを見る
-
相関係数の意味と求め方を分かりやすく解説！
続きを見る
それでは最後まで読んでくださりありがとうございました。
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
