数学Ⅰ「2次関数」の中に『2次関数の決定』という分野がありますね。
今回解決する悩み
「式の置き方が分からない」
今回は2次関数の決定についての悩みを解決します。

この「2次関数の決定」では与えられた条件から2次関数の式を求めます。
与えられる条件とは以下のようなものです。
2次関数の決定
次の条件を満たす2次関数を求めよう。
(1) 頂点が点(4,-3)で、点(2,5)を通る。
(2) 軸が直線\(x=-3\)で、2点(-1,1),(-6,-4)を通る。
(3) 3点(1,10),(-1,2),(-4,5)を通る。
(4) \(x=4\)で最大値6をとり、点(8,-2)を通る。
このような問題に対して、何から手を付けて良いか分からず悩んでいる高校生が多いです。
しかし、そんな高校生に朗報です...✨
実は、2次関数の求め方には3つの型と4つのパターンしかないのです。

本記事では2次関数の式の求め方を解説します。
問題文からどのパターンの問題か分かるようになれば、2次関数の決定は簡単に得点できるのでぜひ最後まで読んで解き方を習得していきましょう。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
2次関数の決定3つの型
2次関数の決定は大きく3つの型に分けられます。

この3つの型を使って問題を解いていくわけですが、問題のパターンは4つしかありません。
問題文の条件からどのパターンなのかを考えます。
①頂点と1点の座標
頂点の座標と他の1点が分かっているときは①の型を使います。
頂点と1点の座標
次の条件を満たす2次関数を求めよう。
頂点が点(-2,4)で,点(-4,2)を通る。

頂点の座標が(-2,4)なので、2次関数が以下の形をしていることが分かります。
\[y=a(x+2)^{2}+4\]
この時点で頭にハテナが浮かんだ方はまず軸と頂点について確認したほうが良いです。
「2次関数の頂点・軸の求め方を分かりやすく解説!」を先にご覧ください。
そして、
\[y=a(x+2)^2+4\]
が点(-4,2)を通る問題なので
\begin{eqnarray}
2&=&a(-4+2)^{2}+4\\
2&=&4a+4\\
4a&=&-2
\end{eqnarray}
よって、
\[\displaystyle a=-\frac{1}{2}\]
したがって求める2次関数は
\[\displaystyle y=-\frac{1}{2}(x+2)^{2}+4\]
だと分かりました。
いまなら公式LINEから簡単なアンケートに答えるだけで、『2次関数』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。
②軸と2点の座標
軸が分かっているときも①の型で求めることができます。
軸と2点の座標
次の条件を満たす2次関数を求めよう。
直線\(x=2\)を軸として、2点(-1,5),(1,-11)を通る。
直線\(x=2\)を軸とするので、2次関数が以下の形をしていることが分かります。
\[y=a(x-2)^{2}+q\]
この2次関数が点\((-1,5),(1,-11)\)を通るから、
\begin{eqnarray}
5&=&a(-1-2)^{2}+q\\
-11&=&a(1-2)^{2}+q
\end{eqnarray}
よって、
\begin{eqnarray}
5&=&9a+q \cdots ①\\
-11&=&a+q \cdots ②
\end{eqnarray}
これを連立方程式で解くと \(a=2,q=-13\)
したがって求める2次関数は
\[\displaystyle y=2(x-2)^{2}-13\]
③3点の座標
通る点の座標が3つ分かっているときは②の型を使います。

3点の座標
2次関数のグラフが3点(2,-2),(3,5),(-1,1)を通るとき、その2次関数を求めよう。
3点が分かっているときは連立方程式を使います。
この2次関数が
点(2,-2)を通るから、\(-2=4a+2b+c \cdots ①\)
点(3,5)を通るので、\(5=9a+3b+c \cdots ②\)
点(-1,1)を通るので、\(1=a-b+c \cdots ③\)
②-①から、\(7=5a+b \cdots ④\)
②-③から、\(4=8a+4b \cdots ⑤\)
④×4-⑤から、\(24=12a\)となり\(a=2\)
④に\(a=2\)を代入すると、\(b=-3\)
①に\(a=2,b=-3\)を代入すると、\(c=-4\)
したがって求める2次関数は
\[y=2x^{2}-3x-4\]
④x軸との交点と1点の座標
x軸との交点が2点と他の1点の座標が分かっているときは③の型です。

x軸の交点と1点の座標
x軸と点(2,0),(5,0)と交わり、点(1,8)を通る2次関数を求めよう。
x軸と点(2,0),(5,0)で交わるので、2次関数が以下の形をしていることが分かります。
\(y=a(x-2)(x-5)\)
この2次関数が点(1,8)を通るので、
\(8=a(1-2)(1-5)\)
\(8=4a\)
\(a=2\)
したがって求める2次関数は
\[y=2(x-2)(x-5)\]
\[y=2x^{2}-14x+20\]
今回は2次関数の式の求め方を解説しましたが、2次関数の公式や重要ポイントをまとめました。
2次関数の決定《練習問題》

今回確認した3つのパターンを活用して、次の練習問題に挑戦しましょう。
練習問題
次の条件を満たす2次関数を求めよう。
(1) 頂点が点(4,-3)で、点(2,5)を通る。
(2) 軸が直線\(x=-3\)で、2点(-1,1),(-6,-4)を通る。
(3) 3点(1,10),(-1,2),(-4,5)を通る。
(4) \(x=4\)で最大値6をとり、点(8,-2)を通る。
練習問題1
練習問題1
次の条件を満たす2次関数を求めよう。
頂点が点(4,-3)で、点(2,5)を通る。
頂点の座標が分かるので2次関数が以下の形をしていることが分かります。
\[y=a(x-4)^{2}-3\]
この2次関数が点(2,5)を通るので、x,yに代入して
\begin{eqnarray}
5&=&a(2-4)^{2}-3\\
5&=&4a-3\\
4a&=&8
\end{eqnarray}
よって、\(\displaystyle a=2\)
したがって求める2次関数は
\[y=2(x-4)^{2}-3\]
練習問題2
練習問題2
次の条件を満たす2次関数を求めよう。
軸が直線\(x=-3\)で、2点(-1,1),(-6,-4)を通る。
軸が\(x=-3\)なので、
\[y=a(x+3)^{2}+q\]
この2次関数が
点(-1,1)を通るから、\(1=a(-1+3)^{2}+q\)
点(-6,-4)を通るので、\(-4=a(-6+3)^{2}+q\)
よって、
\begin{eqnarray}
1&=&4a+q \cdots ①\\
-4&=&9a+q \cdots ②
\end{eqnarray}
これを連立方程式で解くと \(a=-1,q=5\)
したがって求める2次関数は
\[\displaystyle y=-(x+3)^{2}+5\]
練習問題3
練習問題3
次の条件を満たす2次関数を求めよう。
3点(1,10),(-1,2),(-4,5)を通る。
3点が分かっているときは連立方程式を使います。
この2次関数が
点(1,10)を通るから、\(10=a+b+c \cdots ①\)
点(-1,2)を通るので、\(2=a-b+c \cdots ②\)
点(-4,5)を通るので、\(5=16a-4b+c \cdots ③\)
①-②から、\(8=2b \)
よって、\(b=4\)
③-②から、\(3=15a-3b \cdots ④\)
④に\(b=4\)を代入して、\(a=1\)
①に\(a=1,b=4\)を代入すると、\(c=5\)
したがって求める2次関数は
\[y=x^{2}+4x+5\]
練習問題4
練習問題4
次の条件を満たす2次関数を求めよう。
\(x=4\)で最大値6をとり、点(8,-2)を通る。
これはどのパターンでもないように見えますが、\(x=4\)で最大値をとるというのは頂点が点(4,6)であることを表します。
よって、頂点と他の1点の座標が分かっているので①のパターンです。
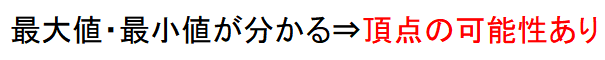
頂点の座標が(4,6)なので2次関数が以下の形をしていることが分かります。
\[y=a(x-4)^{2}+6\]
この2次関数が点(8,-2)を通るので、x,yに代入して
\begin{eqnarray}
-2&=&a(8-4)^{2}+6\\
-2&=&16a+6\\
16a&=&-8
\end{eqnarray}
よって、
\[\displaystyle a=-\frac{1}{2}\]
したがって求める2次関数は
\[\displaystyle y=-\frac{1}{2}(x-4)^{2}+6\]
2次関数のおすすめ勉強法

2次関数は高校数学のなかでも解きやすい問題が多い単元です。
問題の意図をしっかり理解できれば、解法もすぐに思いつけるようになります。
次は2次関数のおすすめ勉強法を紹介します。
- 教科書やノートを見直す
- 問題集で応用力を磨く
- 分かりやすい解説を見る
自分のいまの理解度と目標を照らし合わせて、自分に合った勉強法を試してみてください。

教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。
教科書には重要なポイントがギュッと詰まっています。
2次関数の基本は「2次関数の公式まとめ」にて解説しているのでご覧ください。

問題集で応用力を磨く

2次関数の関する公式に慣れてきたら、次は問題を解いて応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
2次関数の学習におすすめの問題集を紹介します。
Amazon会員なら参考書も読み放題です。
初回30日間の無料体験あり。
⇒参考書が読み放題!Kindle Unlimitedについて詳しく知りたい
分かりやすい解説を見る
以下のような悩みがあるなら映像授業もおすすめです。
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
映像授業なら自分に必要な授業のみを受けられるうえに、分かるまで繰り返し視聴することができます。
分からないを1つずつ解消していけるので、定期テストで高得点を取りたい方は授業授業がおすすめです。
2次関数の決定 まとめ
今回は2次関数の決定についてまとめました。
2次関数の決定2次関数の決定3つの型

問題文からどのパターンなのかを正しく判断できれば、2次関数の決定は決して難しい単元ではありません。
反復練習していけば必ず解けるようになるので学校の問題集でたくさん練習しましょう。
2次関数についてまとめているのでぜひご覧ください。
2次関数を総復習したい方はこちらの記事がおすすめです。
-

基礎から確認!2次関数の公式と重要ポイント
公式LINEから簡単なアンケートに答えるだけで、『2次関数』の重要公式をまとめたPDFをプレゼント中です!








