二項定理の公式と証明をわかりやすく解説！

「二項定理ってなに？」

「二項定理の公式がよく分からない」

二項定理が苦手な方は必見です！

今回は二項定理の公式に関する悩みを解決します。

高校生

二項定理の計算が苦手です...

$悩む学生$

二項定理は「式が長いし、Cが出てくるし、よく分からない」と思っている方も多いですよね。

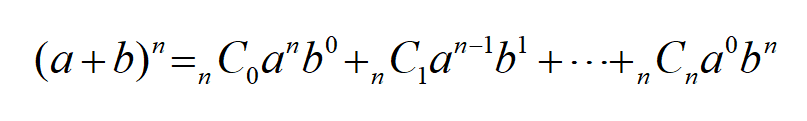
$二項定理公式$

しかし、二項定理は仕組みを理解すればとても単純な式です。

$二項定理の仕組み$

ぼくも始めはニガテでしたが、公式の意味を理解してからは二項定理の計算に困ったことはありません。

本記事では二項定理の公式について解説します。

後半には練習問題もあるので、ぜひ最後までご覧ください。

記事の内容

二項定理の公式
二項定理の使い方
二項定理の証明
二項定理の覚え方
【応用】パスカルの三角形
練習問題
まとめ

この記事を書いた人

$運営者シータ$

シータ

塾講師歴6年
担当した生徒200人以上
（プロフィールで実績公開中）
オンライン家庭教師「スタディトレーナー」運営

$オンライン授業3$

数学を中心としたオンライン家庭教師「スタディトレーナー」生徒募集中！

個別指導のこれ以上ないサポートであなたを支えます。

⇒スタディトレーナー公式サイトはこちら

二項定理の公式

二項定理は以下のような形をしています。

二項定理の公式

\[(a+b)^{n}=_{n}C_{0}a^{n}b^{0}+_{n}C_{1}a^{n-1}b^{1}+_{n}C_{2}a^{n-2}b^{2}+\cdots+_{n}C_{n}a^{0}b^{n}\]

この公式だけ見ると、とても複雑で難しい公式に見えますね。

二項定理はいつ使う？

二項定理は主に$(a+b)^{n}$の展開に使います。

$(a+b)^2$と$(a+b)^3$の展開は二項定理を使わなくてもできますよね。

\begin{eqnarray}
(a+b)^{2}&=&a^{2}+2ab+b^{2}\\
(a+b)^{3}&=&a^{3}+3a^{2}b+3ab^{2}+b^{3}
\end{eqnarray}

では、$(a+b)^4,(a+b)^5,…,(a+b)^{10}$はどうでしょう。

かなり面倒くさいのが分かると思います。

このように次数の高い$(a+b)^{n}$を展開するときに二項定理が役立ちます。

$(a+b)^{n}=_{n}C_{0}a^{n}b^{0}+_{n}C_{1}a^{n-1}b^{1}+_{n}C_{2}a^{n-2}b^{2}+\cdots+_{n}C_{n-1}a^{1}b^{n-1}+_{n}C_{n}a^{0}b^{n}$

二項定理は$(a+b)^5$や$(a+b)^{10}$などを展開するときに大活躍します！

とはいえ、ピンとこないと思うので具体例を見ていきましょう。

高校生

どんな風に役に立つんですか？

二項定理の使い方

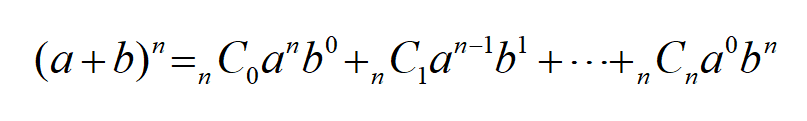
$二項定理公式$

まず初めに$(a+b)^2$を二項定理で展開してみましょう。

つまり、二項定理に$n=2$を代入して考えます。

$n=2$を二項定理に当てはめると、

\begin{eqnarray}
(a+b)^{2}&=&_{2}C_{0}a^{2}b^{0}+_{2}C_{1}a^{2-1}b^{1}+_{2}C_{2}a^{2-2}b^{2}\\
&=&a^2+2ab+b^2 \cdots ①
\end{eqnarray}

$(a+b)^{2}$を分配法則で展開しても、

\[(a+b)^{2}=a^{2}+2ab+b^{2} \cdots ②\]

①,②より、それぞれ同じ項が出てくることが分かりました。

つぎは$(a+b)^5$で試してみましょう。

分配法則で展開していくと

\begin{eqnarray}
(a+b)^{5}&=&(a+b)^{2}(a+b)^{3}\\
&=&(a^{2}+2ab+b^{2})(a^{3}+3a^{2}b+3ab^{2}+b^{3})\\
&=&a^{2}(a^{3}+3a^{2}b+3ab^{2}+b^{3})+2ab(a^{3}+3a^{2}b+3ab^{2}+b^{3})+b^{2}(a^{3}+3a^{2}b+3ab^{2}+b^{3})\\
&=&(a^5+3a^4b+3a^3b^2+a^2b^3)+(2a^4b+6a^3b^2+6a^2b^3+2ab^4)+(a^3b^2+3a^2b^3+3ab^4+b^5)\\
&=&a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5
\end{eqnarray}

分配法則で展開すると、かなり大変な計算になってしまいました。

ここで、$(a+b)^{5}$は二項定理を使います。

$\mathrm{n}=5$とすることで

\begin{eqnarray}
(a+b)^{5}&=&_{5}C_{0}a^5+_{5}C_{1}a^{4}b^{1}+_{5}C_{2}a^{3}b^{2}+_{5}C_{3}a^{2}b^{3}+_{5}C_{4}a^{1}b^{4}+_{5}C_{5}b^{5}\\
&=&a^5+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}
\end{eqnarray}

分配法則で展開するよりも、早く展開することができます。

このように$(a+b)^{n}$の展開をするときに、二項定理が大活躍します。

これで二項定理の便利さはわかってもらえたと思います。

二項定理の公式が頭に入っていれば、$(a+b)^{n}$の展開に怖いものなし！

では、なぜこのような公式になるのか考えましょう。

二項定理の公式《証明》

なぜ二項定理の公式に$\mathrm{C}$が登場するのでしょうか。

展開は文字の組み合わせだからです。

$(a+b)^2$の展開において$a^{2}$の項は

前半の$(a+b)$から$\mathrm{a}$を1つと
後半の$(a+b)$から$\mathrm{a}$を1つ選ぶことで$\mathrm{a^{2}}$が完成します。

こんな調子で(　)から"文字を選ぶ"として考えると

$二項定理の意味を考える$

この中で、$\mathrm{ab}$に注目してみましょう。

$\mathrm{ab}$の項は、$\mathrm{a}$を1つ、$\mathrm{b}$を1つ選んだときに出てきます。

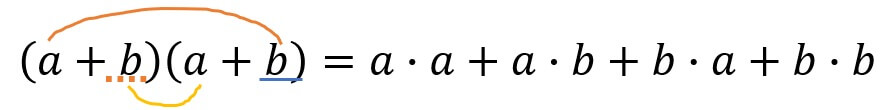
$二項定理の意味を考える$

つまり、$\mathrm{b}$を取り出す$(a+b)$を選ぶと考えて、

\[_{2}C_{1}=2\]

そして、その組み合わせは2通りとなり$2ab$となります。

これが二項定理に$\mathrm{C}$が出てくる正体です。

$(a+b)^5$でも確かめてみましょう。

\[(a+b)^5=(a+b)(a+b)(a+b)(a+b)(a+b)\]

・$a^{5}$は5つの$(a+b)$から0個の$b$を選ぶと考えて、$_{5}C_{0}$通り
⇒　$_{5}C_{0}a^{5}=a^{5}$

・$a^{4}b$は5つの$(a+b)$から1個の$b$を選ぶと考えて、$_{5}C_{1}$通り
⇒　$_{5}C_{1}a^{4}b=5a^{4}b$

・$a^{3}b^{2}$は5つの$(a+b)$から2個の$b$を選ぶと考えて、$_{5}C_{2}$通り
⇒　$_{5}C_{2}a^{3}b^{2}=10a^{3}b^{2}$

・$a^{2}b^{3}$は5つの$(a+b)$から3個の$b$を選ぶと考えて、$_{5}C_{3}$通り
⇒　$_{5}C_{3}a^{2}b^{3}=10a^{2}b^{3}$

・$ab^{4}$は5つの$(a+b)$から4個の$b$を選ぶと考えて、$_{5}C_{4}$通り
⇒　$_{5}C_{4}ab^{4}=5ab^{4}$

・$b^{5}$は5つの$(a+b)$から5個の$b$を選ぶと考えて、$_{5}C_{5}$通り
⇒　$_{5}C_{5}b^{5}=b^{5}$

よって$(a+b)^5$の展開は、

展開する式の次数が大きくなるほど、二項定理のありがたみも大きくなります。

シータ

計算は大変だけど、分配法則で展開するよりもずっと楽だよ。

基礎から丁寧に確認！
プロ講師の分かりやすい解説

ここまで読んで、まだピンと来ていない人いますか？

もしかすると、あなたには文章よりも動画解説のほうが合っているかもしれません。

河合塾が提供する「河合塾One」なら解説が丁寧で、基礎から確認できるのでおすすめです。

しかも、いまなら無料体験で全授業が視聴できます。

<a href="https://px.a8.net/svt/ejp?a8mat=3H9Y57+63OZ02+4ODY+60OXE" target="_blank" rel="noopener">⇒いますぐ「8-5：二項定理」を受講する</a>

二項定理の覚え方

二項定理が覚えられない人は必見です。

二項定理の公式の仕組みを理解すれば、もう困ることはありません。

複雑な二項定理ですが、数字を1つずつ増減させているだけです。

$(x+2)^{3}$を例に見てみましょう。

まずは$C$を書き、右下の数字を1ずつ増加させます。

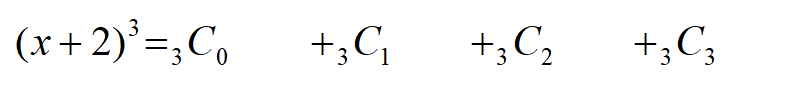
$二項定理の覚え方$

$x$は次数を3から0まで下げていきます。

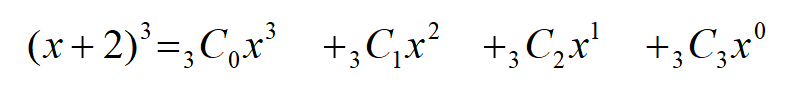
$二項定理の覚え方1$

最後に2の次数を0から3まで増加させます。

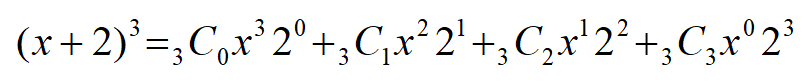
$二項定理の覚え方2$

これで$(x+2)^{3}$を二項定理で計算することができます。

\begin{eqnarray}
(x+2)^{3}&=&_{3}C_{0}x^{3}2^{0}+_{3}C_{1}x^{2}2^{1}+_{3}C_{2}x^{1}2^{2}+_{3}C_{3}x^{0}2^{3}\\
&=&x^{3}+6x^{2}+12x+8
\end{eqnarray}

次は$(x+2)^{4}$でやってみましょう。

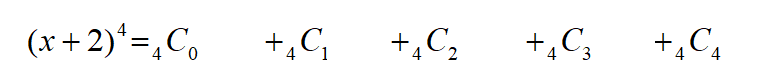
$二項定理の覚え方3$

次数の増減に気を付けましょう。

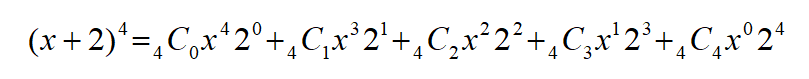
$二項定理の覚え方4$

これで二項定理の公式を作ることができました。

あとは計算すれば完成です。

高校生

こうやって見てみると意外と簡単でした！

式が長くて、文字があるから難しそうに見えちゃうよね

シータ

【応用】パスカルの三角形

「パスカルの三角形」をご存じでしょうか。

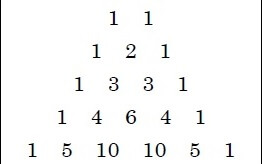
$パスカルの三角形$

上図のような数字の三角形をパスカルの三角形といいます。

各数字は「左上の数と右上の数の和」となっています。

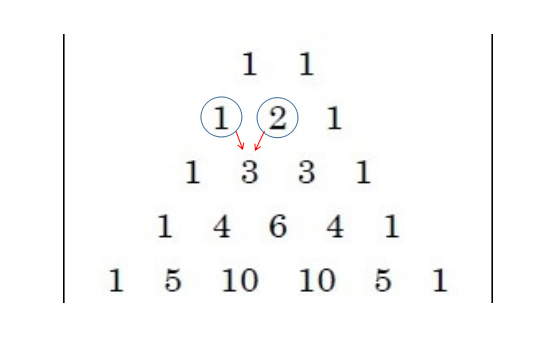
$パスカルの三角形$

パスカルの三角形と$(a+b)^{n}$の展開には深い関わりがあります。

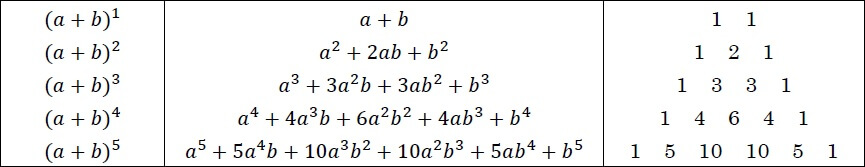
$パスカルの三角形$
$(a+b)^{n}$を展開したとき、各項の係数はパスカルの三角形と同じ規則性があります。

二項定理を忘れたときは、パスカルの三角形で展開をすることもできます。

二項定理《練習問題》

$二項定理<練習問題>$

二項定理を使った練習問題に挑戦しましょう。

練習問題1

次の式を展開しよう。

\[(x+2)^{5}\]

\begin{eqnarray}
(x+2)^{5}&=&_{5}C_{0}x^{5}+_{5}C_{1}x^{4}2^{1}+_{5}C_{2}x^{3}2^{2}+_{5}C_{3}x^{2}2^{3}+_{5}C_{4}x^{1}2^{4}+_{5}C_{5}2^{5}\\
&=&x^{5}+5x^{4} \cdot 2+10x^{3} \cdot 4+10x^{2} \cdot 8+5x \cdot 16+32\\
&=&x^5+10x^{4}+40x^{3}+80x^{2}+80x+32
\end{eqnarray}

したがって、

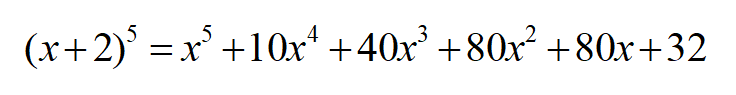
$二項定理の練習問題1$

練習問題2

$(2x-1)^{5}$ の展開式における$x^3$の項の係数を求めよう。

二項定理を活用すると、指定された文字の係数を求めることができます。

以下は二項定理の一般項を表したものです。

$二項定理の項1$

このとき、$x^3$の項が出てくるのは$n=3$のときです。

よって、

\begin{eqnarray}
\displaystyle _{5}C_{2}(2x)^{3}(-1)^{2}&=&\frac{5 \cdot 4}{2 \cdot 1} \cdot 8x^{3} \cdot 1\\
&=&10 \cdot 8x^{3} \cdot 1\\
&=&80x^{3}
\end{eqnarray}

したがって、$x^3$の係数は$80$

二項定理の一般項を使えば、欲しい項だけを取り出すことができます。

二項定理の応用

実は、３項の展開にも公式があります。

3項の展開公式

$(a+b+c)^{n}$の$a^{s}b^{t}c^{r}$の項は

\[\displaystyle \frac{n!}{s!t!r!}abc\]

ただし、$s+t+r=n$

これだけでは理解しづらいので、具体例を見ていきましょう。

例題

$(a+b+c)^{5}$の展開において、$a^{2}b^{2}c$の項の係数を求めよう。

$a^{2}b^{2}c$において指数の和が5になるので、3項の展開公式を使うことができます。

\[\displaystyle \frac{5!}{2!2!1!}a^{2}b^{2}c=30a^{2}b^{2}c\]

したがって、$a^{2}b^{2}c$の項の係数は30であることが分かりました。

3項の展開公式も簡単に証明すると、

$(a+b+c)^{5}=(a+b+c)(a+b+c)(a+b+c)(a+b+c)(a+b+c)$なので

５つの$(a+b+c)$から$a$を取り出す(　)を２つ選ぶ

⇒$_{5}C_{2}a^{2}$

残りの3つ$(a+b+c)$から$b$を取り出す(　)を２つ選ぶ

⇒$_{3}C_{2}b^{2}$

最後に残り1つの$(a+b+c)$から$c$を取り出すので

⇒$_{1}C_{1}c$

ゆえに、$a^{2}b^{2}c$の係数は

\[_{5}C_{2}a^{2}\times_{3}C_{2}b^{2}\times_{1}C_{1}c\]

これは次のように式変形することができます。

\begin{eqnarray}
\displaystyle _{5}C_{2}a^{2}\times_{3}C_{2}b^{2}\times_{1}C_{1}c&=&\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2!2!1!}a^{2}b^{2}c\\
&=&\frac{5!}{2!2!1!}a^{2}b^{2}c
\end{eqnarray}

したがって、3項の展開における各項の係数を以下の計算で求めることができます。

\[\displaystyle \frac{5!}{2!2!1!}=30\]

このように3項の展開公式も便利です。この機会にぜひ覚えておいてください。

二項定理の公式　まとめ

今回は二項定理の公式についてまとめました。

二項定理　まとめ

二項定理の公式とは以下のような公式です。

二項定理の公式

\[(a+b)^{n}=_{n}C_{0}a^{n}b^{0}+_{n}C_{1}a^{n-1}b^{1}+_{n}C_{2}a^{n-2}b^{2}+\cdots+_{n}C_{n}a^{0}b^{n}\]

二項定理の計算に$C$が含まれるのは、組み合わせの考え方をしているからです。

$二項定理の意味を考える$

二項定理を用いることで以下のメリットがあります。

展開の計算が早くなる
展開式における係数が求められる

今回は二項定理に焦点を当てて解説しました。

二項定理は一見すると難しそうな公式ですが、数字を1ずつ増減させていくだけの単純な計算です。

二項定理も使えるようにしたいですが、3乗の展開公式は暗記しておきましょう。

3乗の展開公式はこちらの記事で解説しました。

$【三乗の展開公式】(a±b)3乗の展開公式と覚え方を解説！$: 【三乗の公式】(a±b)3乗の展開公式と覚え方を解説！

数学ⅡBのまとめ記事へ

定期テストにおすすめな映像授業

河合塾One

基本から学びたい方には河合塾Oneがおすすめ！
AIが正答率を判断して、あなただけのオリジナルカリキュラムを作成してくれます！
まずは7日間の無料体験から始めましょう！

詳細ページへ

無料体験から始める

スタディサプリ

会員数157万人の業界No.1の映像授業サービス。
月額2,178円で各教科のプロによる授業が受け放題！分からないところだけ学べるので、学習効率も大幅にUP！
本気で変わりたいならすぐに始めよう！

詳細ページへ

無料体験から始める

要チェック！

「どうして勉強したのに点数が下がるの...」

勉強しているのに成績が上がらない方は「【体験談】偏差値40から60まで上げたぼくの勉強法」を必見！

$偏差値40から60に上げたぼくの勉強法$: 【やれば上がるはウソ】偏差値40から60まで上げたぼくの勉強法！

二項定理の公式と証明をわかりやすく解説！