今回解決する悩み
「ベクトルの垂直ってなに?」
「垂直なベクトルはどうやって求めるの?」
今回は数学Bのベクトルから「ベクトルの垂直条件」に関するこんな悩みを解決します。

2つのベクトルが垂直のとき、以下の式が成り立ちます。
ベクトルの垂直条件
0ではない2つのベクトル\(\vec{a}、\vec{b}\)があります。
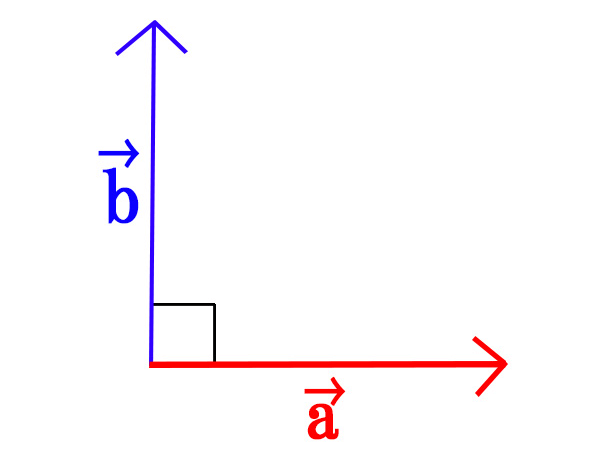
2つのベクトルが垂直な関係にあるとき、内積\(\vec{a} \cdot \vec{b}=0\)となり、以下の式が成り立つ。
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1})、\vec{b}=(x_{2},y_{2})\)のとき、
\begin{eqnarray}
\vec{a} \bot \vec{b} &\Leftrightarrow& \vec{a} \cdot \vec{b}=0\\
&\Leftrightarrow& x_{1}x_{2}+y_{1}y_{2}=0
\end{eqnarray}
「垂直だったら内積0」として覚えておきましょう!
今回はベクトルの垂直条件について詳しく解説していきます。
内積との関係や、練習問題を使いながら分かりやすく説明していきますので、苦手意識を持っている方も、ぜひ最後まで読んでみてくださいね!
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。

ライター紹介
国公立の教育大学を卒業
数学講師歴8年目に突入
教えた生徒の人数は300人以上
それではベクトルの垂直条件について解説していきましょう。
ベクトルの垂直条件
0ではない2つのベクトル\(\vec{a}、\vec{b}\)があります。

2つのベクトルが垂直な関係にあるとき、内積\(\vec{a} \cdot \vec{b}=0\)となります。
ベクトルの垂直条件
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1})、\vec{b}=(x_{2},y_{2})\)のとき、
\begin{eqnarray}
\vec{a} \bot \vec{b} &\Leftrightarrow& \vec{a} \cdot \vec{b}=0\\
&\Leftrightarrow& x_{1}x_{2}+y_{1}y_{2}=0
\end{eqnarray}
参考
ベクトルの内積\(\vec{a} \cdot \vec{b}\)については別の記事で解説しています。
-

ベクトルの内積の公式と求め方を分かりやすく解説!
続きを見る
垂直条件の証明
先ほど紹介した垂直条件について、証明していきます。
ベクトルの垂直条件は以下でした。

0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1})、\vec{b}=(x_{2},y_{2})\)のとき、
\begin{eqnarray}
\vec{a} \bot \vec{b} &\Leftrightarrow& \vec{a} \cdot \vec{b}=0…①\\
&\Leftrightarrow& x_{1}x_{2}+y_{1}y_{2}=0…②
\end{eqnarray}
まず、\(\vec{a}\bot\vec{b}\Leftrightarrow\vec{a} \cdot \vec{b}=0\)…①を証明していきます。
次に、\(\vec{a} \cdot \vec{b}=0\Leftrightarrow x_{1}x_{2}+y_{1}y_{2}=0\)…②の証明については、内積の定義で簡単に説明がつきます。
aベクトルに垂直な単位ベクトル
ここからは垂直な単位ベクトルについて解説します。
よく出題される問題で「あるベクトルに垂直な単位ベクトルを求めなさい。」という問題があるので必ず押さえておきましょう。
まずは、単位ベクトルについて復習しましょう。
単位ベクトルとは、下図のような大きさが1のベクトルです。
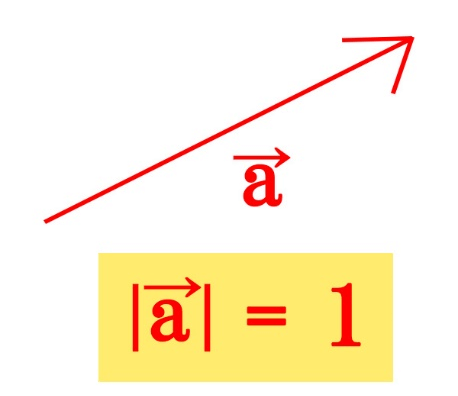
単位ベクトルの定義をおさえながら、例題を見ていきます。
単位ベクトルの例題
\(\vec{a}=(2,1)\)と垂直な単位ベクトル\(\vec{t}=(x,y)\)を求めましょう。
単位ベクトルですので、\(|\vec{t}|=1\)であることから、
\[x^{2}+y^{2}=1\]
参考
\(\vec{t}=(x,y)\)のとき
\[|\vec{t}|=\sqrt{x^{2}+y^{2}}\]
また、\(\vec{t}\)が\(\vec{a}\)と垂直であるとき、2つのベクトルの内積は0になります。
よって、
\begin{eqnarray}
\vec{a} \cdot \vec{t}&=&0\\
\left(2,1\right) \cdot \left(x,y\right)&=&0\\
2x+y&=&0\\
y&=&-2x
\end{eqnarray}
先ほどの、\(x^{2}+y^{2}=1\)を使って、
\begin{eqnarray}
x^{2}+{(-2x)}^{2}&=&1\\
5x^{2}&=&1\\
\displaystyle x^{2}=\frac{1}{5}\\
\displaystyle x&=&\pm \frac{1}{\sqrt5}\\
\displaystyle x&=&\pm \frac{\sqrt5}{5}
\end{eqnarray}
したがって、求める単位ベクトルは、
\(\displaystyle \vec{t}=(\frac{\sqrt5}{5},-\frac{2\sqrt5}{5}),(-\frac{\sqrt5}{5},\frac{2\sqrt5}{5})\)
となる。
1つのベクトルに対して垂直なベクトルは2つありますので、両方とも答えになります。


垂直条件を用いた練習問題
ここからは、垂直条件を絡めたベクトルの練習問題を紹介していきます。
丁寧に解説していきますので、ぜひ一緒に解いてみましょう。
練習問題①
練習問題①
\(\vec{a}=(2,-1),\vec{b}=(5,k)\)とする。
このとき、\(\vec{a},\vec{b}\)が互いに垂直となるような\(k\)の値を求めよう。
練習問題②
練習問題①
\(\vec{a}=(k,1),\vec{b}=(k,k-6)\)とする。
\(\vec{a},\vec{b}\)が互いに垂直であり、\(|\vec{a}|=\sqrt{10}\)となるような、\(k\)の値を求めよう。

ベクトルの平行条件
垂直条件にあわせて、ベクトルの平行条件も知っておきましょう。
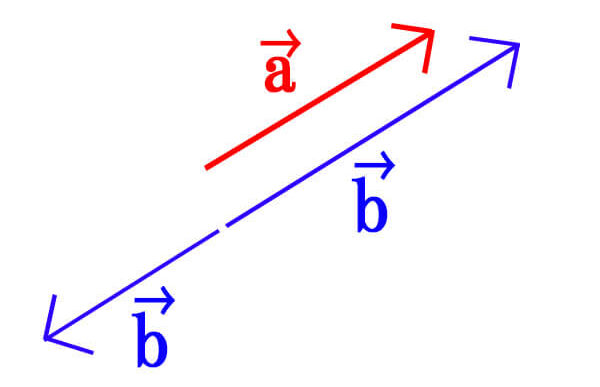
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、
\[\vec{a}//\vec{b}\Leftrightarrow\vec{b}=k\vec{a}\]
となる実数kがある。
また、
\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0\]
別記事では、この平行条件について詳しく解説していますので、ぜひチェックしてみてください。
ベクトルの垂直条件 まとめ
今回はベクトルの垂直条件について学習しました。
まとめ
ベクトルの垂直条件
0ではない2つのベクトル\(\vec{a}、\vec{b}\)があります。

2つのベクトルが垂直な関係にあるとき、内積\(\vec{a} \cdot \vec{b}=0\)となり、以下の式が成り立つ。
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1})、\vec{b}=(x_{2},y_{2})\)のとき、
\begin{eqnarray}
\vec{a} \bot \vec{b} &\Leftrightarrow& \vec{a} \cdot \vec{b}=0\\
&\Leftrightarrow& x_{1}x_{2}+y_{1}y_{2}=0
\end{eqnarray}
ベクトルの垂直条件でも内積は欠かせないので「ベクトルの内積」についてもしっかりと理解しておく必要があります。
ベクトルの内積はこちらの記事で詳しく解説しています。
-

ベクトルのなす角を求める方法!平面・空間どちらもマスターしよう!
続きを見る
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!







