数学B数列の中で「等比数列」は必ず押さえておきたい数列です。
今回解決する悩み
「等比数列の基礎から知りたい」
「等比数列の一般項って?」
「等比数列の和の求め方は?」
今回は等比数列に関する悩みを解決していきます。

等比数列とは「一定の比で変化する数列」を指します。

等比数列は数列のなかでも基本となる数列です。
一般項や和を求める問題が多く出題されるので、しっかり理解していないと数列の単元は苦戦するでしょう。
本記事では等比数列の一般項と和の公式について解説します。
数列が苦手な方や、これから数列を学習する方の参考になるので、ぜひ最後までご覧ください。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
等比数列とは?
等比数列とは「一定の比で変化する数列」を指します。
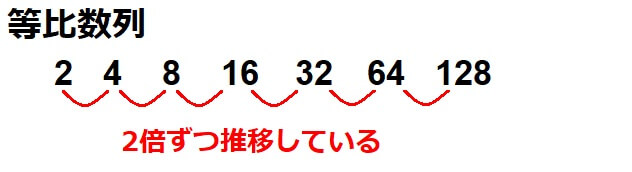
数列の初めの項を初項、最後の項を末項といいます。
また、等比数列において隣り合う2つの項の比を公比といいます。

以下のような数列があるとします。

上記の数列は『初項2、末項486、公比3、項数6の等比数列』といいます。
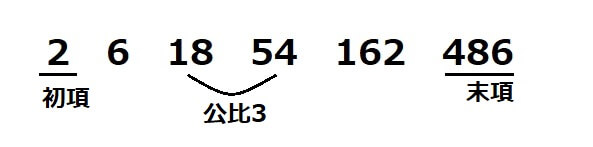
等比数列
等比数列 ⇒ 一定の比で変化する数列
公比:隣り合う項の比
初項:最初の項
末項:最後の項
等比数列を一般項で表す
等比数列の一般項の公式
一般項とは、数列の第\(n\)項\(a_{n}\)を\(n\)を用いて表したものです。
等比数列の一般項は以下の式で表します。
等比数列の一般項
初項\(a_{1}\)、公比\(r\)の等比数列\(\{a_{n}\}\)とすると、
\[a_{n}=a_{1} \cdot r^{n-1}\]


等比数列の一般項の証明
等比数列は初項に対して公比を掛けていく数列です。
数列\(a_{1} a_{2} a_{3} a_{4} ... a_{n}\)が等比数列だとします。
この等比数列の公比を\(r\)だとすると、
\(a_{1}=a_{1}\)←初項
\(a_{2}=a_{1} \times r\)
\(a_{3}=a_{1} \times r^{2}\)
\(a_{4}=a_{1} \times r^{3}\)
このように初項に公差を加えていくので、
\(a_{1}=a_{1}\)
\(a_{2}=a_{1} \times r\)
\(a_{3}=a_{1} \times r^{2}\)
:
\(a_{n}=a_{1} \times r^{n-1}\)
したがって、等比数列の一般項は\(a_{n}=a_{1} \cdot r^{n-1}\)となります。

等比数列の一般項を求める
等比数列の一般項を求める例を見てみましょう。
ここに等比数列があります。
2 , 6 , 18 , 54 , 162 …
この数列は「初項2、公比3の等比数列」です。
ここで等比数列の一般項の公式を思い出してみましょう。
等比数列の一般項
初項\(a_{1}\)、公比\(d\)の等比数列を\(\{a_{n}\}\)とすると、
\(a_{n}=a_{1} \cdot r^{n-1}\)
この数列は初項2、公比3の数列なので、
\begin{eqnarray}
a_{n}&=&a_{1} \times r^{n-1}\\
&=&2 \times 3^{n-1}\\
&=&2 \cdot 3^{n-1}
\end{eqnarray}
したがって、等比数列{2 , 6 , 18 , 54 , 162 …}の一般項は\(a_{n}=2 \cdot 3^{n-1}\)

求めた一般項が不安なときは具体的な数字を代入して確かめます。
初項が2なので、一般項に\(n=1\)を代入して2になれば大丈夫です。
\begin{eqnarray}
a_{1}&=&2 \times 3^{1-1}\\
&=&2 \times 1\\
&=&2
\end{eqnarray}
\(n=1\)のとき初項と同じ値になったので間違いなさそうです。
等比数列の和
等比数列の和の公式
数列の項を足すことを数列の和といいます。
等比数列{3 , 6 , 12 , 24}の初項から第4項までの和は26となります。
3+6+12+24=45
このように等比数列の和を求める問題はよく出題されます。
等比数列の和の公式は公比の値によって変わります。複雑ですが確実に覚えておきたい公式です。
等比数列の和
初項\(a\)、公差\(d\)、項数\(n\)の等比数列の和を\(S_{n}\)とすると、
[1]\(r < 1\)のとき
\[\displaystyle S_{n}=\frac{a(1-r^{n})}{1-r}\]
[2]\(r > 1\)のとき
\[\displaystyle S_{n}=\frac{a(r^{n}-1)}{r-1}\]
[3]\(r=1\)のとき
\[S_{n}=na\]
実際に等比数列の和を2つのやり方で求めてみます。
等比数列の和の公式①
このような等比数列があったとしましょう。

この数列は「初項5、公比3、項数6の等比数列」です。
公比が3で1より大きいのでこの公式を使います。
\[\displaystyle S_{n}=\frac{a(r^{n}-1)}{r-1}\]
初項5、公比3、項数6の等比数列の和は
\begin{eqnarray}
\displaystyle S_{6}&=&\frac{a(r^{n}-1)}{r-1}\\
&=&\frac{5(3^{6}-1)}{3-1}\\
&=&\frac{5(729-1)}{2}
&=&1820
\end{eqnarray}
したがって、等比数列の和を求めることができました。
等比数列の和の公式
公比\(r\)が1より大きい場合はこの公式で求める。
\[\displaystyle S_{n}=\frac{a(r^{n}-1)}{r-1}\]
等比数列の和の公式②
公比が1の場合の等比数列の和を求めましょう。
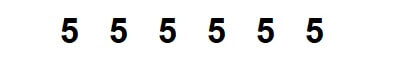
\(r = 1\)の場合は同じ数字が並び続ける数列です。
この数列の和は(初項)×(項数)で求めることができます。
したがって、\(r=1\)のときはこの公式を使いましょう。
\[\displaystyle S_{n}=na\]
今回は初項5、項数6の等比数列なので、
\begin{eqnarray}
\displaystyle S_{6}&=&5 \times 6\\
&=&30
\end{eqnarray}
等比数列の和の公式
公比\(r\)が1の場合はこの公式で求める。
\[\displaystyle S_{n}=na\]

等比数列のΣ
そもそもΣ(シグマ)とは
Σ(シグマ)とは数学の記号の1つです。
数列\(a_{n}\)の初項から第\(n\)項まで足すことを記号Σ(シグマ)を用いて、以下のように表します。
\[\sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+a_{3}+\cdots+a_{n}\]
\(\sum_{k=1}^{n}\)の見た目が難しそうなので身構えてしまいますが、シグマの意味は「k=1からnまで代入したものを足す」というだけです。
シグマΣの公式や計算については「Σシグマの計算公式と証明!数列の和が一瞬で解ける!」で解説しています。
等比数列のΣ
以下のようなΣの計算は、等比数列の和として考えることができます。
等比数列のΣ
\[\sum_{k=1}^{n} r^{k}=\displaystyle \frac{r(r^{n}-1)}{r-1}= \frac{r(1-r^{n})}{1-r}\]
なぜこのΣの計算が等比数列の和になるのかを解説します。
まず左辺のΣを計算してみると、
\[\sum_{k=1}^{n} r^{k}=r+r^{2}+r^{3}+ \cdots + r^{n}\]
となります。
これは「初項r、公比r、項数nの等比数列の和」と同じ形をしていますね。
そこで右辺は等比数列の和の公式で表すことができるので、
\begin{eqnarray}
\sum_{k=1}^{n} r^{k}&=&r+r^{2}+r^{3}+ \cdots + r^{n}\\
\displaystyle &=&\frac{r(r^{n}-1)}{r-1}
\end{eqnarray}
これで等比数列のΣを和で表すことができるのです。
等比数列のΣの計算
では、1問だけΣの計算をしてみましょう。
等比数列のΣ
次の値を求めてみよう。
\[\sum_{k=1}^{6} 3^{k}\]
これが意味するのは、\(\{3+9+27+\cdots+729\}\)なので、「初項3、末項729、項数6の等比数列の和」として考えると、
\begin{eqnarray}
\sum_{k=1}^{6} 3^{k}&=&3+9+27+ \cdots + 729\\
\displaystyle &=&\frac{3(3^{6}-1)}{3-1}\\
\displaystyle &=&\frac{3(729-1)}{2}\\
&=&1092
\end{eqnarray}
Σの計算公式を知らないと、和\(S_{n}\)や群数列で苦戦することになります。

Σシグマの計算公式と証明!数列の和が一瞬で解ける!
等比数列の漸化式
等比数列の漸化式は以下のような形で表します。
等比数列の漸化式
数列における第\(n\)項を\(a_{n}\)、公比を\(r\)とすると、
\[a_{n+1}=ra_{n}\]
漸化式とは、数列の第\(n\)項\(a_{n}\)を用いて次の項である\(a_{n+1}\)を表した式です。
等比数列の漸化式は、\(a_{n}\)に公比\(r\)を掛けることで\(a_{n+1}\)になることを表しています。
実際に数字を入れて考えてみましょう。

ここに初項2、公比3の等比数列があります。
この数列は初項に対して、3倍ずつ変化していくので
\(a_{1}=2\)
\(a_{2}=3 \cdot a_{1}\)
\(a_{3}=3 \cdot a_{2}\)
\(a_{4}=3 \dot a_{3}\)
という関係が成り立ちます。
このように\(a_{n+1}\)の項を表すときは、\(a_{n}\)を3倍すれば良いので、
\[a_{n+1}=3a_{n}\]
したがって、等比数列の漸化式は以下の形で表される。
等比数列の漸化式
数列における第\(n\)項を\(a_{n}\)、公比を\(r\)とすると、
\[a_{n+1}=ra_{n}\]
等比数列の性質
等比数列の性質の1つに”等比中項”というものがあります。
等比中項
数列\(a,b,c\)が等比数列のとき、
\[b^{2}=ac\]
これは等比数列の項3つ用意したときに、両端の項の積が中央の項の2乗になることを意味します。
証明は非常に簡単です。\(a,b,c\)は等比数列なので
\[\displaystyle \frac{b}{a}=\frac{c}{b}\]
両辺にabを掛けて、
\[b^{2}=ac\]
となります。
その他の数列
今回は等比数列について解説しています。
数列には等比数列以外にも以下の数列があります。
- 等差数列
- 階差数列
・等差数列
等差数列とは、「一定の差で変化する数列」を指します。

等差数列については、「等差数列の公式まとめ!一般項と和の公式を分かりやすく解説!」で詳しく解説しています。
・階差数列
階差数列は複雑で、各項の差を書き出してみるとある数列が見えてきます。
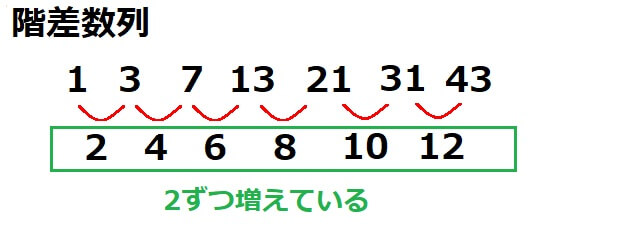
上の数列の場合、各項の差が等差数列になっています。
この差が等比数列になる場合もありますし、もっと複雑な数列になるときもあります。
階差数列については、「階差数列を用いた一般項と和を求める公式!初項に階差を足していくだけ」で解説しています。
等比数列《練習問題》
等比数列の一般項や和の求め方を確認しました。
実際に数字を使って、一般項や和を求めてみましょう。
練習問題1
次の数列の一般項を求めよう。
2, 10 , 50 , 250 , 1250 …
練習問題2
次の数列の初項から第\(n\)項までの和を求めよう。
3 , 6 , 12 , 24 , 48 …
等比数列 まとめ
今回は等比数列について詳しく解説しました。
等比数列 まとめ
等比数列とは
⇒一定の比で変化する数列
等比数列の一般項
初項\(a_{1}\)、公比\(r\)の等比数列\(\{a_{n}\}\)とすると、
\[a_{n}=a_{1} \cdot r^{n-1}\]
等比数列の和の公式
初項\(a\)、公差\(d\)、項数\(n\)の等比数列の和を\(S_{n}\)とすると、
[1]\(r < 1\)のとき
\[\displaystyle S_{n}=\frac{a(1-r^{n})}{1-r}\]
[2]\(r > 1\)のとき
\[\displaystyle S_{n}=\frac{a(r^{n}-1)}{r-1}\]
[3]\(r=1\)のとき
\[S_{n}=na\]
本記事では等比数列をメインに解説しましたが、等差数列や階差数列も重要な数列です。
この3つの数列は確実に押さえておかないと、漸化式や群数列を学習するときに苦戦するでしょう。
それぞれの数列については別の記事で解説しています。
合わせて読みたい
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。








