数学Bの数列で出てくる「∑(シグマ)」に悩まされる高校生も多いはず。
今回解決する悩み
「シグマの公式が分からない」
「数列のシグマの計算が苦手」
今回は数列のシグマに関する悩みを解決します。

数列の和を求める問題など、さまざまな所でΣ(シグマ)を使います。
まず前提の知識として、Σ(シグマ)とは総和を表す記号で、
\[\displaystyle \sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+ \cdots +a_{n}\]
を表しています。
例えば、\(\displaystyle \sum_{k=3}^{10} a_{k}\)のときは、\(a_{n}\)のn=3からn=10までの足し算を意味します。
\[\displaystyle \sum_{k=3}^{10} a_{k}=a_{3}+a_{4}+ \cdots +a_{10}\]
そんなシグマには絶対に覚えておきたい5つの公式があります。
Σの計算公式
本記事ではΣシグマの計算公式と性質について解説します。
Σの計算ができないのは公式を覚えていない場合が多いです。本記事を読んで、ぜひ覚えてしまいましょう。
目次
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
Σシグマの計算公式
Σシグマを学習するにあたって、確実に覚えておきたい公式が5つあります。
Σの計算公式
どれも重要な公式なので、必ず覚えましょう。
シグマの計算公式の証明は「4. Σシグマの公式の証明」で解説します。

Σシグマの性質
Σシグマの計算公式と合わせて、以下の性質も覚えておきましょう。
Σシグマの性質
\(p,q\)は定数とすると、
\(\displaystyle 1.\sum_{k=1}^{n}(a_{k}+b_{k})=\sum_{k=1}^{n} a_{k}+\sum_{k=1}^{n} b_{k}\)
\(\displaystyle 2.\sum_{k=1}^{n} pa_{k}=p\sum_{k=1}^{n} a_{k}\)
1,2より
\(\displaystyle \sum_{k=1}^{n}(pa_{k}+qb_{k})=p\sum_{k=1}^{n} a_{k}+q\sum_{k=1}^{n} b_{k}\)
それぞれの性質について証明します。
Σシグマの性質①の証明
Σシグマの性質②の証明
数列\(\{a_{n}\}\)に対して、\(p\)を定数とすると
\(\displaystyle \sum_{k=1}^{n} pa_{k}\)
\(\displaystyle =pa_{1}+pa_{2}+\cdots+pa_{n}\)
\(\displaystyle =p(a_{1}+a_{2}+\cdots+a_{n})\)
\(\displaystyle =p\sum_{k=1}^{n} a_{k}\)
Σシグマの性質③の証明
以上のΣの計算公式と性質を利用すれば、様々な数列の和も求めることができます。


Σシグマを利用する問題
Σシグマの基本問題
実際に公式や性質を使って、いくつか問題を解いてみましょう。
まずは超基本となる計算問題から
Σシグマの基本問題
次の計算をしてみよう。
\(\displaystyle 1.\sum_{k=1}^{n} 3k\)
\(\displaystyle 2.\sum_{k=1}^{n} (k^{2}+2k)\)
\(\displaystyle 3.\sum_{k=1}^{n} 3 \cdot 2^{k}\)
(1)の解説
(1)の問題は定数の3を前に出すことで、Σの計算公式②の等差数列の和が使えます。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} 3k&=&3 \sum_{k=1}^{n} k\\
\displaystyle &=&3 \cdot \frac{1}{2}n(n+1)\\
\displaystyle &=&\frac{3}{2}n(n+1)
\end{eqnarray}
使った公式
\[\displaystyle \sum_{k=1}^{n} k=\frac{1}{2}n(n+1)\]
(2)の解説
使った公式
\[\displaystyle \sum_{k=1}^{n} k=\frac{1}{2}n(n+1)\]
\[\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\]
(3)の解説
(3)の問題は計算公式⑤で紹介した等比数列の和として考えます。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} 3 \cdot 2^{k}&=&3 \sum_{k=1}^{n} 2^{k}\\
\displaystyle &=&3 \cdot \frac{2(2^{n}-1)}{2-1}\\
\displaystyle &=&6(2^{n}-1)
\end{eqnarray}
等差数列や等比数列の和の公式をまだ覚えてない人はすぐに確認しましょう!


一般項を求めてから和を求める問題
以下のような一般項を求めてから和を求める問題もあります。
数列の和
次の数列の初項から第\(n\)項までの和を求めよう。
\[1 , 6 , 11 , 16 , 21 , …\]
この問題はまず数列の一般項\(a_{n}\)を求める必要があります。
なぜなら、一般項で表すことでΣの計算ができるようになるからです。
1 , 6 , 11 , 16 , 21 , …
与えられた数列は「初項1、公差5の等差数列」です。
したがって、一般項\(a_{n}\)は
\begin{eqnarray}
a_{n}&=&1+5(n-1)\\
&=&5n-4
\end{eqnarray}
一般項が分かればあとはΣの計算をするだけです。
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} a_{k}&=&\sum_{k=1}^{n} (5k-4)\\
\displaystyle &=&5 \sum_{k=1}^{n} k - \sum_{k=1}^{n} 4\\
\displaystyle &=&5 \cdot \frac{1}{2}n(n+1) - 4n\\
\displaystyle &=&\frac{1}{2}n(5n-3)
\end{eqnarray}
したがって、与えられた数列の初項から第\(n\)項までの和を求めることができました。
参考
等差数列の一般項の求め方は「等差数列の一般項と和の公式を分かりやすく解説!」で解説しています。
-

階差数列を用いた一般項と和を求める公式!初項に階差を足していくだけ
数列の一般項を求める
数列の一般項を求めるときにもΣを使います。

数列\(\{a_{n}\}\)の隣り合う項の差でできた数列\(\{b_{n}\}\)を階差数列といいます。
もとの数列の一般項\(a_{n}\)を求めるには、初項\(a_{1}\)に対して階差数列\(\{b_{n}\}\)を加えるイメージで考えます。
\(a_{1}=a_{1}\) ←初項
\(a_{2}=a_{1}+b_{1}\)
\(\displaystyle a_{3}=a_{2}+b_{2}=a_{1}+\sum_{k=1}^{2} b_{k}\)
\(\displaystyle a_{4}=a_{3}+b_{3}=a_{1}+\sum_{k=1}^{3} b_{k}\)
:
\(\displaystyle a_{n}=a_{n-1}+b_{n-1}=a_{1}+\sum_{k=1}^{n-1} b_{k}\)
したがって、元の数列の一般項\(a_{n}\)は
\[\displaystyle a_{n}=a_{n-1}+b_{n-1}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]
で求めることができます。
階差数列については「階差数列を用いた一般項と和を求める公式!」で詳しくまとめました。
分数の和は部分分数分解
以下のような分数の和はシグマではなく部分分数分解で解きます。

なんだか難しそうと思った方も多いですよね。
部分分数分解とは、以下のように1つの分数を分解することを指します。
部分分数分解
\[\displaystyle \frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}\]
部分分数分解を利用すると、与えられた分数の和も
それぞれの分数が符号の違うもの同士で相殺するので、シンプルな答えになります。


4. Σシグマの公式の証明
「1.Σシグマの計算公式」で紹介したΣシグマの公式を証明します。
証明を読まない方は飛ばしてもらって大丈夫なところです。
Σシグマの計算公式
公式の証明①
\(a\)が\(k\)を含んでいないので\(\displaystyle \sum_{k=1}^{n} a\)というのは、\(a\)を\(n\)回足すことを意味します。
したがって、
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} a&=&a+a+ \cdot + a\\
&=&an
\end{eqnarray}
公式の証明②
\[\displaystyle \sum_{k=1}^{n} k=1+2+3+\cdots +n\]
これは「初項1、末項\(n\)、項数\(n\)の等差数列の和」を表しています。
右辺を等差数列の和の公式に置き換えて
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} k&=&1+3+ \cdot + n\\
\displaystyle &=&\frac{1}{2}n(n+1)
\end{eqnarray}
公式の証明③
恒等式
\[(k+1)^{3}-k^{3}=3k^{3}+3k+1\]
を利用します。
\(k=1,2,3,\cdots,n\)とすると
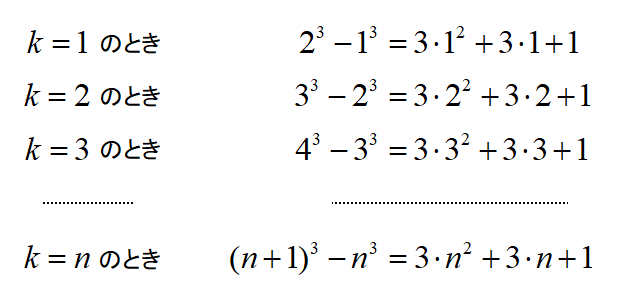
これらの式の両辺を加えると、
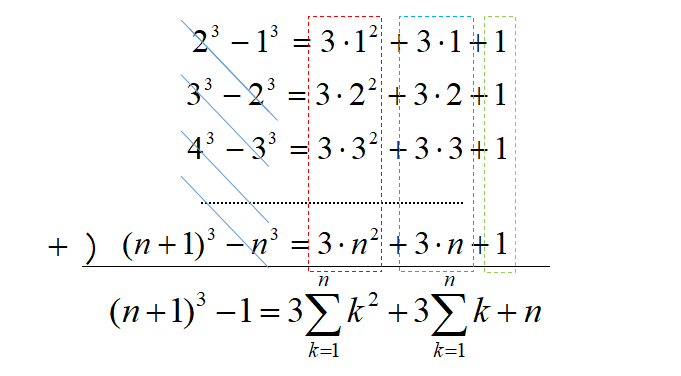
これらを移項して、
\[\displaystyle 3\sum_{k=1}^{n} k^{2}=(n+1)^{3}-1-3\sum_{k=1}^{n} k -n\]
ここで\(\displaystyle \sum_{k=1}^{n} k =\frac{1}{2}n(n+1)\)を代入して
最後に両辺を3で割って、
\[\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\]
公式の証明④
恒等式
\[(k+1)^{4}-k^{4}=4k^{3}+6k^{2}+4k+1\]
を利用します。
\(k=1,2,3,\cdots,n\)とすると
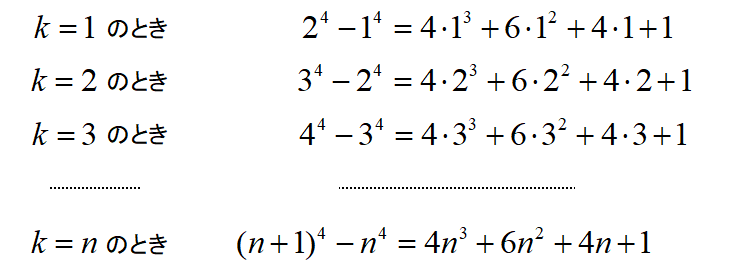
これらの式の両辺を加えると、
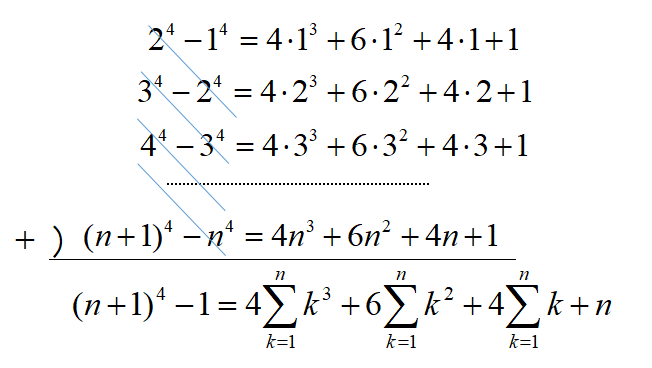
これらを移項して、
ここで
\(\displaystyle \sum_{k=1}^{n} k =\frac{1}{2}n(n+1)\)
\(\displaystyle \sum_{k=1}^{n} k^{2}=\frac{1}{6}n(n+1)(2n+1)\)
を代入して、式を整理すると、
\[\displaystyle 4\sum_{k=1}^{n} k^{3}=n^{2}(n+1)^{2}\]
最後に両辺を4で割って、
\[\displaystyle \sum_{k=1}^{n} k^{3}=\{\frac{1}{2}n(n+1)\}^{2}\]
公式の証明⑤
\[\displaystyle \sum_{k=1}^{n} ar^{k-1}=a+ar+\cdots +ar^{n-1}\]
これは「初項\(a\)、公比\(r\)、項数\(n-1\)の等比数列の和」を表しています。
右辺を等比数列の和の公式に置き換えると
\begin{eqnarray}
\displaystyle \sum_{k=1}^{n} ar^{k-1}&=&a+ar+\cdots +ar^{n-1}\\
\displaystyle &=&\frac{a(r^{n}-1)}{r-1} (r > 0)\\
\displaystyle &=&\frac{a(1-r^{n})}{1-r} (r < 0)
\end{eqnarray}
公式の証明はできなくても問題ないので、まずは5つの公式を確実に使えるようになりましょう。
《重要》3つの基本数列
今回はΣシグマの公式や性質について解説しました。
シグマは数列の和を求めるときに活躍しますが、そもそも数列の一般項を求められないとシグマを活用できません。
以下の数列はかなり重要なので確実に押さえておきましょう。
基本の数列
- 等差数列
- 等比数列
- 階差数列
・等差数列
等差数列とは、「一定の差で変化する数列」を指します。

・等比数列
等比数列とは、「初めの項に一定の数をかけ続けていく数列」を指します。
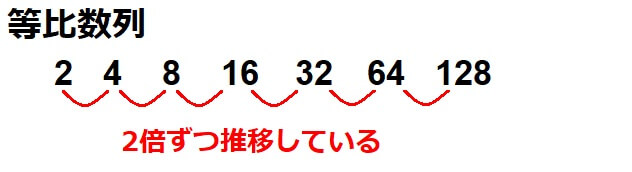
・階差数列
階差数列は複雑で、各項の差を書き出してみるとある数列が見えてきます。
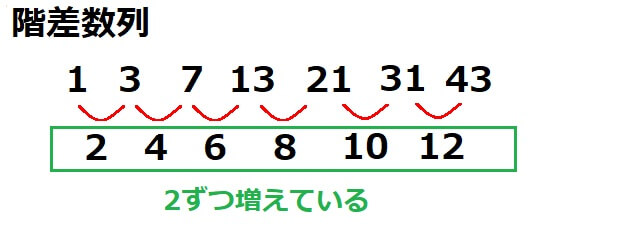
上の数列の場合、各項の差が等差数列になっています。
この差が等比数列になる場合もありますし、もっと複雑な数列になるときもあります。
数Bの数列についてまとめ記事を作りました。
基礎から確認したい方はぜひご覧ください。
-

【数列の公式まとめ】等差・等比・階差・漸化式・群数列を徹底解説!
Σシグマの公式 まとめ
今回はΣシグマの計算公式や性質についてまとめました。
Σシグマの公式 まとめ
Σの計算公式
Σシグマの性質
\(p,q\)は定数とすると、
\(\displaystyle 1.\sum_{k=1}^{n}(a_{k}+b_{k})=\sum_{k=1}^{n} a_{k}+\sum_{k=1}^{n} b_{k}\)
\(\displaystyle 2.\sum_{k=1}^{n} pa_{k}=p\sum_{k=1}^{n} a_{k}\)
1,2より
\(\displaystyle \sum_{k=1}^{n}(pa_{k}+qb_{k})=p\sum_{k=1}^{n} a_{k}+q\sum_{k=1}^{n} b_{k}\)
数列の単元は覚えることは多いですが、問題のパターンが限られています。
それぞれの性質や公式をしっかりと覚えれば、数列はベクトルよりも得点しやすい単元です。


Σの計算がスムーズにできると、数列の和や群数列の問題でも素早く解くことができます。
各数列の性質や、漸化式、群数列について知りたい方は「数列まとめ記事」をご覧ください。
-

【数列の公式まとめ】等差・等比・階差・漸化式・群数列を徹底解説!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。








