今回解決する悩み
「三角関数をひと通り復習したい」
「三角関数の公式を確認したい」

三角関数は覚える公式が多く、習ったばかりだと難しく感じる単元の1つです。
定期テストだけでなく、共通テストにも必ず出題されるのでしっかり理解してきましょう。
| 2023年共通テスト数学ⅡB | ||
| 第1問 | [1] | 三角関数 |
| [2] | 指数関数・対数関数 | |
| 第2問 | [1][2] | 微分法と積分法 |
| 第3問 | 確率分布と統計的な推測 | |
| 第4問 | 数列 | |
| 第5問 | ベクトル | |
本記事では、三角関数で使う公式を網羅的に学べるようにまとめました。
苦手な部分だけでなく、分かったつもりでいる部分も確認してみてください。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
三角関数の基本
まずは超基本の三角比の公式から確認します。
まず単位円と呼ばれる原点\(O\)を中心とした半径\(r\)の円を描きます。
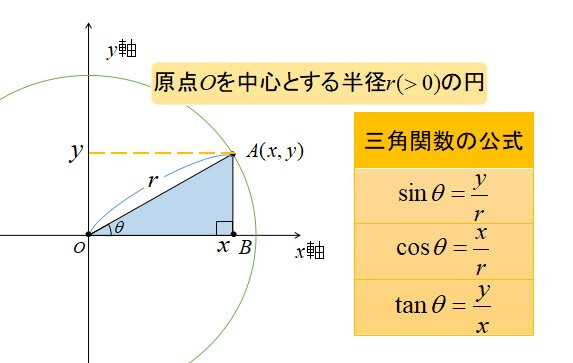
\(x\)軸の正の方向に対して、線分\(OA\)による角の大きさを\(\angle AOB=\theta \)とするとき、
三角比の公式
\[\sin \theta = \frac{y}{r}, \cos \theta = \frac{x}{r}, \tan \theta = \frac{y}{x}\]
上記の三角比を含んだ関数を三角関数といいます。
三角比の求め方は以下の3通りの動きで覚えましょう。
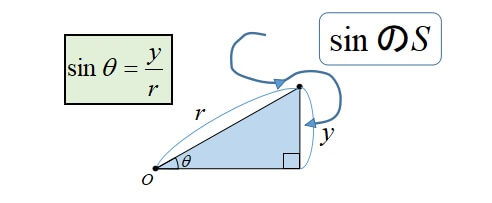
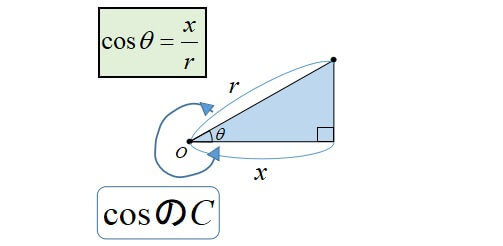
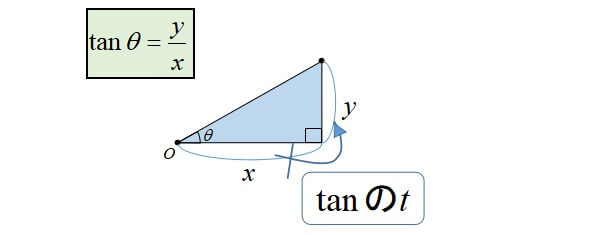
詳しくは「三角比(sin,cos,tan)の公式と覚え方」で解説しているので、合わせてどうぞ。
弧度法(ラジアン)とは?
三角関数を習うと角度を弧度法で表すようになります。
「弧度法ってなんだよ。」
「ラジアンってなに!?」
そんな声が聞こえてきそうですね(笑)
弧度法というのは、”弧”に注目して角度を表現する方法のことです。
円の半径と弧の長さが等しくなる角度を1rad(ラジアン)といいます。
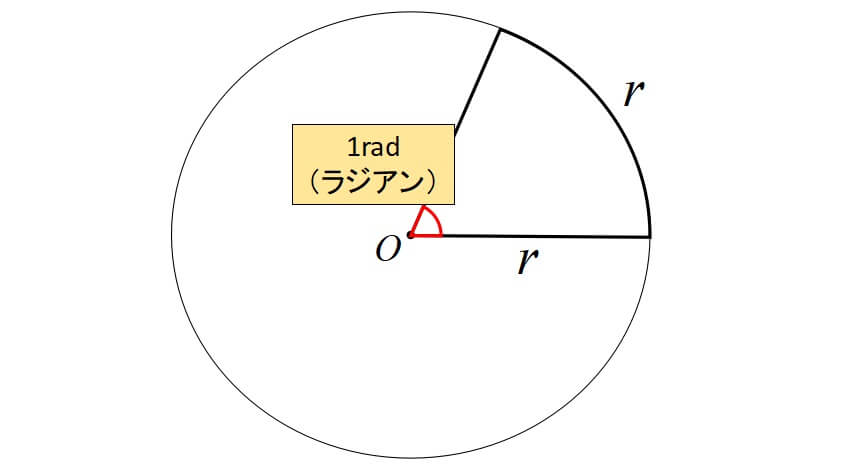
半径\(r\)の円において、円周の長さは\(2\pi r\)となり、この時の中心角を\(2\pi\)ラジアンといいます。
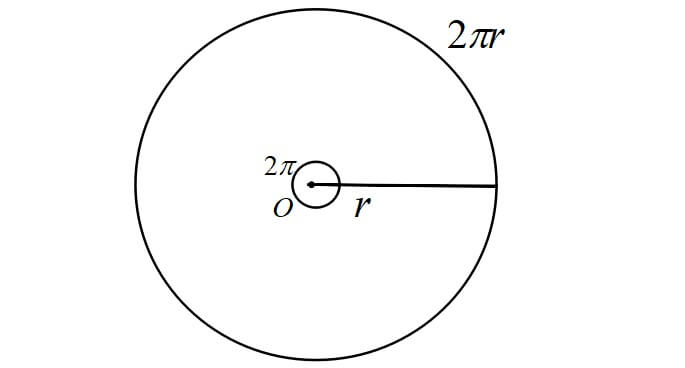
詳しくは「弧度法とは?弧度法の変換や面積公式すべて解説!」
三角比の相互関係

三角比は\(\sin,\cos,\tan\)のいずれか1つが分かるだけで、その他の三角比も分かります。
それには以下の三角比の相互関係がとても重要になってきます。
三角比の相互関係は必ず押さえておきたい公式です。
三角比の相互関係
\(\sin^{2} \theta+\cos^{2} \theta = 1\)
\(\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}\)
\(\displaystyle 1+\tan ^{2} \theta = \frac{1}{\cos ^{2} \theta}\)
三角関数の相互関係については詳しく知りたい方は「三角関数の相互関係」をご覧ください。
\(\theta+\pi\)の公式
\(sin(\theta+\pi)\)のような角度の部分に\(\pi\)を含む公式をまとめました。
公式①
\(\sin =-\sin \theta\)
\(\cos (-\theta)=\cos \theta\)
\(\tan (-\theta)=-\tan \theta\)
公式②
\(\displaystyle \sin (\theta+\frac{\pi}{2})=\cos \theta\)
\(\displaystyle \cos (\theta+\frac{\pi}{2})=-\sin \theta\)
\(\displaystyle \tan (\theta+\frac{\pi}{2})=-\frac{1}{\tan \theta}\)
公式③
\(\sin (\theta+\pi)=-\sin \theta\)
\(\cos (\theta+\pi)=-\cos \theta\)
\(\tan (\theta+\pi)=\tan \theta\)
詳しくは「θ+π/2,θ+π三角関数の公式と導き方」
加法定理を活用した公式
次は三角形の加法定理についてまとめます。
加法定理を活用して様々な公式が成り立っているので、加法定理を理解しておくと考え方の幅が広がります。
加法定理
まずは加法定理から確認しましょう。
加法定理を使うことで、\(\displaystyle \sin \frac{5}{12}\pi\)などの三角比を求めることができます。
加法定理
\begin{eqnarray}
\sin(\alpha+\beta)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(\alpha-\beta)&=&\sin \alpha \cos \beta-\cos \alpha \sin \beta\\
\cos(\alpha+\beta)&=&\cos \alpha \cos \beta-\sin \alpha \sin \beta\\
\cos(\alpha-\beta)&=&\cos \alpha \cos \beta+\sin \alpha \sin \beta\\
\displaystyle \tan(\alpha+\beta)&=&\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\
\displaystyle \tan(\alpha-\beta)&=&\frac{\tan \alpha -\tan \beta}{1+\tan \alpha \tan \beta}
\end{eqnarray}
加法定理の重要ポイントは「加法定理の公式まとめ!加法定理の重要ポイントを徹底解説!」にまとめました。
式が長く加法定理が覚えられない!という方は、語呂合わせで覚えてしまいましょう。
2倍角の公式
2倍角の公式
\begin{eqnarray}
\sin 2 \theta &=& 2 \sin \theta \cos \theta\\
\cos 2 \theta &=& \cos ^{2} \theta-\sin ^{2} \theta\\
&=& 2 \cos ^{2} \theta-1\\
&=& 1-2 \sin ^{2} \theta\\
\displaystyle \tan 2 \theta &=& \frac{2 \tan \theta}{1-\tan ^{2} \theta}
\end{eqnarray}
2倍角の定理は先ほど紹介した加法定理を変形して証明できます。
非常によく使う公式なので、公式を丸暗記してしまうことをオススメします。
-

2倍角の公式と求め方!cosの変形をマスターしよう!
3倍角の公式
3倍角の公式も載せておきましょう。
3倍角の公式
\begin{eqnarray}
\sin 3 \theta &=&-4 \sin ^{3} \theta+3 \sin \theta\\
\cos 3 \theta &=&4 \cos ^{3} \theta-3 \cos \theta\\
\displaystyle \tan 3 \theta &=&\frac{3 \tan \theta - \tan ^{3} \theta}{1-3 \tan ^{2} \theta}
\end{eqnarray}
-

3倍角の公式と覚え方!公式をマスターして得点アップ!
半角の公式
半角の公式は2倍角の公式を利用して半角の三角関数を導く公式です。
ただし、2倍角や3倍角の公式と違って、2乗の形であることに注意が必要です。
半角の公式
\begin{eqnarray}
\displaystyle \sin ^{2} \frac{\theta}{2}=\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}=\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}=\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}
-

半角の公式と証明・導き方を解説!もう公式を忘れても大丈夫!
三角関数の合成

三角関数の合成は初めて見たとき驚きますよね。
「どうしてそうなった!?」
そんな風に感じました。
三角関数の合成公式
\(a\)と\(b\)のいずれかが\(0\)でないとき
\(a \sin \theta+b \cos \theta=\sqrt{a^{2}+b^{2}} \cos (\theta-\alpha)\)
ただし, \(\alpha\)は\(\displaystyle \sin \alpha=\frac{b}{\sqrt{a^{2}+b^{2}}},\cos \alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\) を満たす角度とする。
三角関数の合成の証明や練習問題は「三角関数の合成公式と証明!sin・cosの合成を徹底解説!」にまとめました。
三角関数の和積・積和の公式
三角関数の和や積の形を変換する公式を和積の公式や積和の公式といいます。
積和の公式
まずは積和の公式から!
積和の公式
積和の公式は加法定理を用いて、導くことができます。
和積の公式
次は三角比の和を積で表す、和積の公式です。
和積の公式は先ほど紹介した積和の公式から導かれます。
和積の公式
和積の公式・積和の公式は本当に覚えづらい公式なので、どうしても覚えられない方は「和積&積和の公式と覚え方」を参考にしてみてください。
三角関数を利用した公式

その他にも三角関数を利用した公式がいくつかあるので紹介します。
正弦定理
正弦定理は三角形に使う定理です。
各頂点A,B,Cとして、向かい合う辺をa,b,cとする。
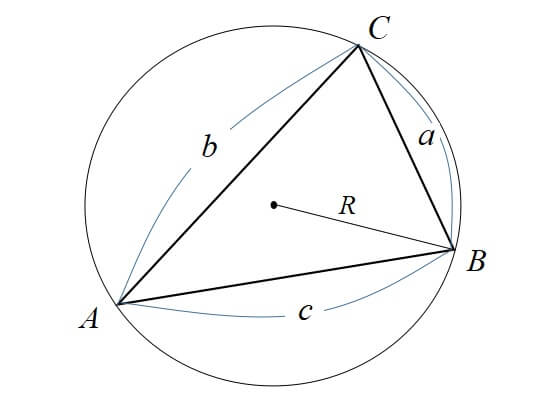
正弦定理
△ABCの外接円の半径をRとすると、次が成り立つ。
\[\displaystyle \frac{a}{sin A}=\frac{b}{sin B}=\frac{c}{sin C}=2R\]
-

正弦定理の公式と使い方を徹底解説!これでもう迷わない!
余弦定理
余弦定理も三角形に辺や角を求められる定理です。
各頂点A,B,Cとして、向かい合う辺をa,b,cとする。
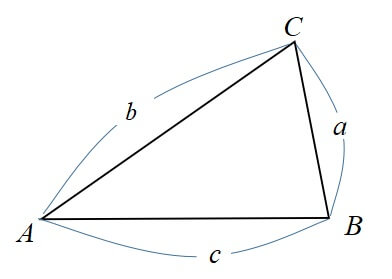
余弦定理
△ABCにおいて、次が成り立つ。
\begin{eqnarray}
a^{2} &=& b^{2}+c^{2}-2bc \cos \angle A\\
b^{2} &=& a^{2}+c^{2}-2ac \cos \angle B\\
c^{2} &=& a^{2}+b^{2}-2ab \cos \angle C
\end{eqnarray}
-

余弦定理の公式と証明!分かりやすく図を使って解説
sinを使った面積公式
三角関数を使って三角形の面積を求めることもできるんです。
sin(サイン)を用いた面積公式は三角形の2辺とその間の角が分かってるときに使うことができます。
sinを用いた面積公式
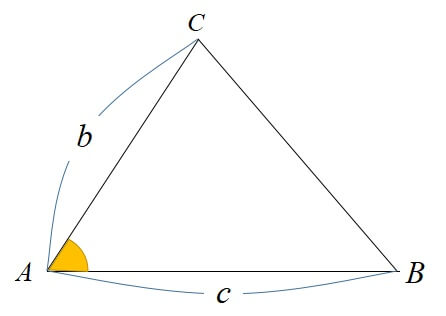
2辺の長さとその間の角が分かれば三角形\(ABC\)の面積\(S\)を求めることができます。
\begin{eqnarray}
S &=& \frac{1}{2}bc \sin A \\
&=& \frac{1}{2}ca \sin B \\
&=& \frac{1}{2}ab \sin C
\end{eqnarray}
-

三角形の面積公式!三角比sinを用いて面積を求めよう!
2直線のなす角と傾きの関係
tan(タンジェント)を用いて2直線のなす角の大きさを求めることもできます。
2直線のなす角と傾き互いに垂直でない2直線
\[y=m_{1} x+n_{1}, \quad y=m_{2} x+n_{2}\]
のなす角を \(\theta\) として
\[\displaystyle \tan \theta=|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}|\]
-

2直線のなす角と傾きの関係を解説!
三角関数のまとめ
今回は三角関数についてそれぞれまとめました。
簡単な説明と公式を載せただけなので、詳しい解説は各記事の詳細をご覧ください。
三角関数以外の単元についてもまとめ記事を出しています。
マストラでは高校生の教科書に沿った解説記事を載せているので、定期試験前の確認に活用して下さい。
ぼくがたった4ヶ月で偏差値を19上げることができた体験談はこちら
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。













