「2直線のなす角ってどうやって求める?」
今回はこんな生徒さんに向けて記事を書いていきます。
2つの直線を引くと、2直線の間に角がうまれますよね。
その角の大きさを傾きを使って求める公式があるんです。
今回は2直線のなす角と傾きの関係を解説していきます。
ぜひ最後まで見ていってね!
・2直線のなす角と傾きの関係
・2直線のなす角と傾きの関係 証明
・<練習問題>
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
2直線のなす角と傾きの関係

2直線のなす角と傾き互いに垂直でない2直線
\(y=m_{1} x+n_{1}, \quad y=m_{2} x+n_{2}\)
のなす角を \(\theta\) として
\(\displaystyle \tan \theta=|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}|\)
そもそも2直線がなす角というのは、直線を2本引いたときに交点ができますね。
そのときにできるこの角度のことを2直線がなす角といいます。
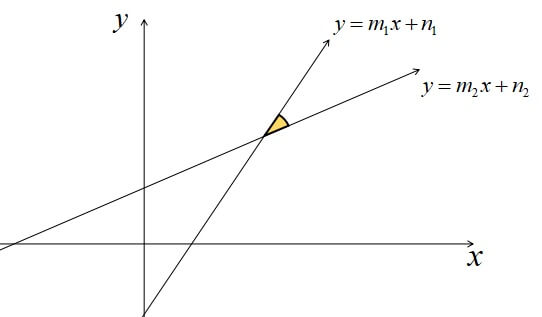
例えば2直線
\(y=\sqrt{3} x+2\)
\(y=(2−\sqrt{3})x−1\)
が存在するとき、この2直線のなす角は
\(m_{1}=\sqrt{3}, \quad m_{2}=2−\sqrt{3}\)
\(\displaystyle \tan \theta=|{\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}}|\)
\(\displaystyle =|\frac{\sqrt{3}-(2-\sqrt{3})}{1+\sqrt{3}(2-\sqrt{3})}|\)
\(\displaystyle =|\frac{2\sqrt{3}-2}{2\sqrt{3}-2}|\)
\(\displaystyle =1\)
\(\tan \theta=1\)より\(\theta=45^\circ\)
このように、2直線のなす角と傾きの関係を用いることで、角の大きさを求めることができます。
2直線のなす角と傾きの証明

2直線のなす角と傾きの関係を証明していきます。
使っているのは、\(\tan \theta\)の加法定理です。
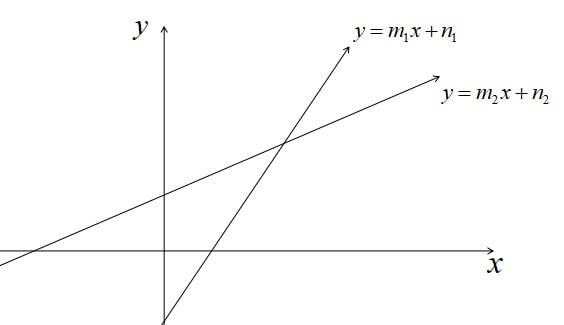
2直線を
\(y=m_{1} x+n_{1}, \quad y=m_{2} x+n_{2}\)
として、それらを原点を通るように平行移動すると
\(y=m_{1} x, \quad y=m_{2} x\)
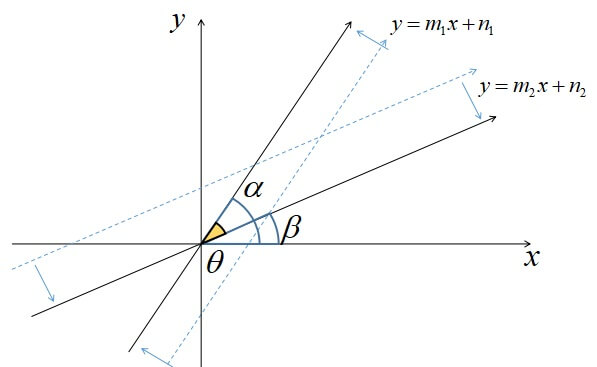
それぞれ \(x\)軸の正の部分となす角を\(α , β\)とすると、
\(tan α=m_{1},\quad tan β=m_{2}\)
となります。
ここで2直線がなす角は
\(\theta=α-β\)
となるので
\(\displaystyle \tan \theta=|\tan(α-β)|\)
\(\displaystyle =|\frac{\tan α-\tan β}{1+\tan α \tan β}|\)
\(\displaystyle =|\frac{m_{1}-m_{2}}{1+m_{1}m_{2}}|\)
<練習問題>

では、2直線のなす角と傾きの関係を用いた練習問題を用意しました。
\(\displaystyle y=-\frac{\sqrt{3}}{5} x+2, \quad y=\frac{\sqrt{3}}{2} x+1\)
解説
\(\displaystyle m_{1}=-\frac{\sqrt{3}}{5}, \quad m_{2}=\frac{\sqrt{3}}{2}\)
\(\displaystyle \tan \theta=|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}|\)
\(\displaystyle =|\frac{-\frac{\sqrt{3}}{5}-\frac{\sqrt{3}}{2}}{1+(-\frac{\sqrt{3}}{5}) \times \frac{\sqrt{3}}{2}}|\)
\(\displaystyle =|\frac{-\frac{\sqrt{3}}{5}-\frac{\sqrt{3}}{2}}{1-\frac{3}{10}}|\)
\(\displaystyle =|\frac{-\frac{2\sqrt{3}}{10}-\frac{5\sqrt{3}}{10}}{1-\frac{3}{10}}|\)
\(\displaystyle =|\frac{-2\sqrt{3}-5\sqrt{3}}{10-3}|\)
\(\displaystyle =|\frac{-7\sqrt{3}}{7}|\)
\(\displaystyle =|-\sqrt{3}|\)
\(\tan \theta=\sqrt{3}\)より\(\theta=60^\circ\)
したがって、2直線
\(\displaystyle y=-\frac{\sqrt{3}}{5} x+2, \quad y=\frac{\sqrt{3}}{2} x+1\)
がなす角の大きさは\(60^\circ\)
おわりに
今回は数学Ⅱの三角関数から2直線のなす角と傾きの関係についてまとめました。
他にも、教科書に内容に沿ってどんどん解説記事を挙げていきます。
お気に入り登録しておいてもらえると、定期試験前や入試勉強をするときに確認できます。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。






