今回は命題と条件に関する悩みを解決していきます。
- 命題ってなに？
- 否定とは？
- 逆、裏、対偶の意味が曖昧
ここが曖昧な生徒が多いので、一緒にしっかりと理解をしておきましょう！
きっと感じているほど難しくないので、理解しておかないともったいない
今回は命題の意味に加え、「否定」「逆・裏・対偶」の意味も紹介します。
・命題とは？
・仮定と結論
・否定とは
・逆・裏・対偶
ライター紹介
国公立の教育大学を卒業
数学講師歴6年目に突入
教えた生徒の人数は150人以上
高校数学のまとめサイトを作成中
命題とは？
命題とは「正しいか正しくないかが定まる文章または式」です。
命題は正しいか正しくないかが明確に判断できます。
命題の例
- \(x=3\)ならば\(2x=6\)である
- 自然数4は偶数である
- ライオンは生き物である
命題でない文章は正しいか判断をすることができません。
命題でない例
- 1000は大きい数である
- 車は速い
- 東京はすごい
命題が正しいとき、その命題は真であるといいます。
命題が正しくないとき、その命題は偽であるといいます。
仮定と結論
命題の「～ならば」を仮定、「～である」を結論といいます。
例えば、実数についての命題「3より大きいならば、1より大きい」は真の命題です。
「3より大きいならば」が仮定で、「1より大きい」が結論です。
ここで仮定と結論を実数\(x\)に関する2つの条件に置き換えると
仮定 \(p:x>3\)
結論 \(q:x>1\)
これらを用いて「pならばq」と表現することができます。
このような命題を \(p \Rightarrow q\)と書きます。
否定とは
否定とは「条件の文章や式を打ち消すもの」です。
言葉にすると分かりづらいですが、名前の通り否定するだけです。
条件：「xは有理数である」
否定：「xは有理数ではない」すなわち「xは無理数である」
条件：「\(x>0\)」
否定：「\(x>0\)でない」すなわち「\(x \leq 0\)」
条件\(p\)の否定は条件\(\overline{p}\)と書きます。
逆・裏・対偶の関係
命題には「逆」「裏」「対偶」の３つの関係があります。
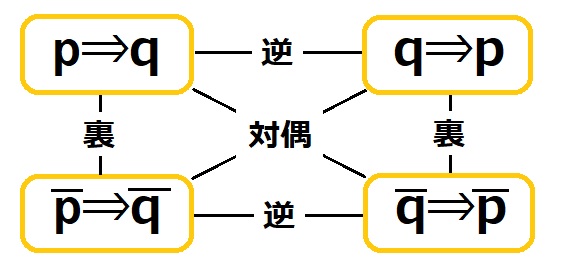
命題\(p \Rightarrow q\)に対して、
- 逆：\(q \Rightarrow p\)
- 裏：\(\overline{p} \Rightarrow \overline{q}\)
- 対偶：\(\overline{q} \Rightarrow \overline{p}\)
命題「nは6の倍数 \(\Rightarrow\) nは3の倍数」のとき、逆・裏・対偶は以下のようになります。
| 命題 | nは6の倍数 \(\Rightarrow\) nは3の倍数 |
|---|---|
| 逆 | nは3の倍数 \(\Rightarrow\) nは6の倍数 |
| 裏 | nは6の倍数ではない \(\Rightarrow\) nは3の倍数ではない |
| 対偶 | nは3の倍数の倍数ではない \(\Rightarrow\) nは6の倍数ではない |
命題「nは6の倍数 \(\Rightarrow\) nは3の倍数」は真の命題ですが、逆と裏は偽です。
命題の真偽が「逆」と「裏」の真偽と一致するとは限らないので確認が必要です。
ここで覚えておいてほしいのが、「対偶の真偽は命題の真偽と一致する」ことです。
対偶「nは3の倍数の倍数ではない \(\Rightarrow\) nは6の倍数ではない」は真の命題です。
与えられた命題の真偽を証明するとき、対偶の真偽を確かめる方法で証明することもできます。
命題 まとめ
今回は数と式から命題と条件についてまとめました。
正しいか正しくないかが定まる文章または式仮定と結論命題の「～ならば」の部分を仮定、「～である」の部分を結論といいます。
逆・裏・対偶
命題\(p \Rightarrow q\)に対して、
- 逆：\(q \Rightarrow p\)
- 裏：\(\overline{p} \Rightarrow \overline{q}\)
- 対偶：\(\overline{q} \Rightarrow \overline{p}\)
他にも、教科書に内容に沿った解説記事を挙げています。
お気に入り登録して定期試験前に確認してください。
最後まで読んでくださりありがとうございました。
みんなの努力が報われますように！
2021年映像授業ランキング
スタディサプリ
会員数157万人の業界No.1の映像授業サービス。
月額2,178円で各教科のプロによる授業が受け放題！分からないところだけ学べるので、学習効率も大幅にUP！
本気で変わりたいならすぐに始めよう！
