加法定理の証明を分かりやすく解説！2点の距離と余弦定理で示めす

「加法定理の証明が知りたい」
「どうして加法定理は成り立つの？」
今回は加法定理に関するこんな悩みを解決します。

高校生

加法定理がなぜ成り立つのか知りたいです

三角関数のなかでも加法定理は重要な公式の1つです。

加法定理

\begin{eqnarray}
\sin(α+β)&=&\sin \alpha \cos \beta + \cos \alpha \sin \beta\\
\sin(α-β)&=&\sin α \cosβ-\cosα \sinβ\\
\cos(α+β)&=&\cos α \cosβ-\sinα \sinβ\\
\cos(α-β)&=&\cos α \cos β+\sinα \sinβ\\
\displaystyle \tan(α+β)&=&\frac{\tanα+\tanβ}{1-\tanα \tanβ}\\
\displaystyle \tan(α-β)&=&\frac{\tanα-\tanβ}{1+\tanα \tanβ}
\end{eqnarray}

見た目が複雑な形をしているので、

「加法定理はどうしてそんな公式になるの？」

そう思う方もいるかもしれません。

本記事では加法定理の証明をまとめました。

実はそこまで難しい証明ではないので、ぜひ最後までご覧ください。

記事の内容

加法定理の証明
- 余弦定理を使う証明
- 余弦定理を使わない証明
まとめ

※本ページは学習アプリのプロモーションが含まれています。

シータ

気になる見出しをクリックして、
ぜひ最後までご覧ください。

▲スマホから数学の質問ができる
学習アプリ『Rakumon』

アプリをダウンロードする

24時間いつでもチャットで解決！

加法定理の証明

加法定理を全て証明するには、

\[\cos(α+β)=\cos α \cosβ-\sinα \sinβ\]

をまず証明します。

\(\cos(α+β)\)を証明するにはいくつか方法がありますが、今回は定番の2つを紹介します。

余弦定理を用いて証明
余弦定理を用いない証明

さっそく加法定理を証明していきましょう！

シータ

証明方法はいろいろ知っておくと良いよ！

加法定理の証明：余弦定理を使う

まずは余弦定理を用いて加法定理を証明します。

点\(P,Q\)の座標を\(P(\cos \alpha ,\sin \alpha),Q(\cos \beta ,\sin \beta)\)とします。

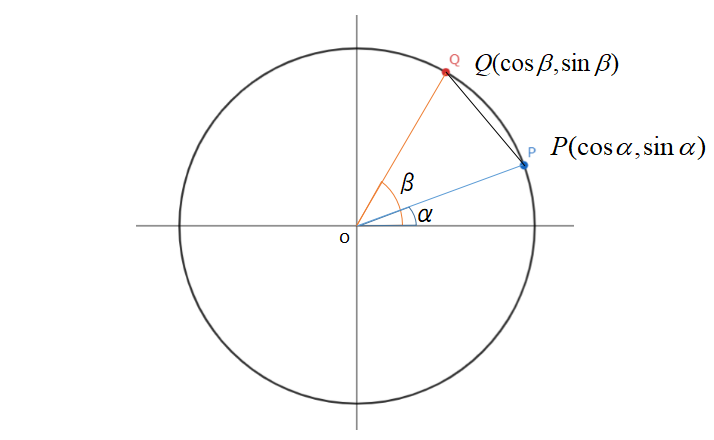
まずは余弦定理を用いて\(PQ^{2}\)を表します。

点\(P,Q\)は単位円上の点なので、\(OP=OQ=1\)です。

\begin{eqnarray}
PQ^{2}&=&OP^{2}+OQ^{2}-2OP \cdot OQ \cos (\beta - \alpha)\\
&=&1+1-2\cos(\beta - \alpha)\\
&=&2-2 \cos(\alpha - \beta) \cdots ①
\end{eqnarray}

次に点\(P\)と点\(Q\)の2点間の距離をもとめて、

\begin{eqnarray}
PQ^{2}&=&(\cos \beta -\cos \alpha)^{2}+(\sin \beta -\sin \alpha)^{2}\\
&=&2-2\cos \alpha \cos \beta - 2 \sin \alpha \sin \beta\\
&=&2-2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) \cdots ②
\end{eqnarray}

①,②より、

\[2-2 \cos(\alpha - \beta)=2-2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)\]

ゆえに、

\[2 \cos(\alpha - \beta)=2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)\]

したがって、

\[\cos(\alpha - \beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta\]

加法定理の証明：余弦定理を使わない

次に余弦定理を使わないで証明をしていきます。

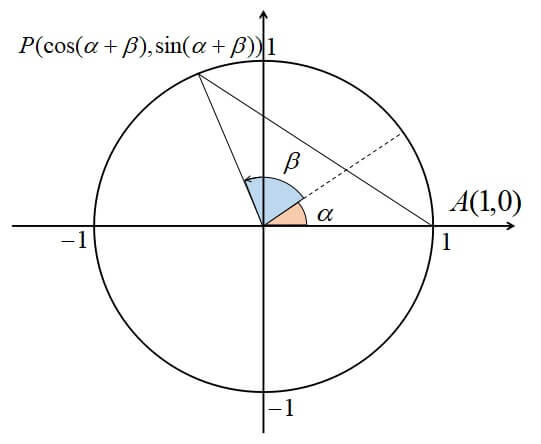
上の図において、\(AP\)間の距離を求めると

\begin{eqnarray}
AP^{2}&=&\{\cos(\alpha + \beta)-1\}^{2}+\sin^{2}(\alpha + \beta)\\
&=&2-2\cos (\alpha + \beta)
\end{eqnarray}

次に、２点\(P,A\)を原点を中心に\(- \alpha\)だけ回転した位置にある点を、それぞれ\(Q,R\)とする。

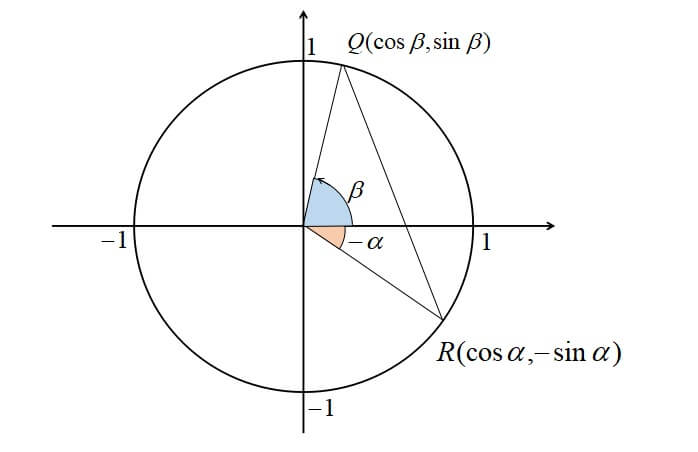
\(Q,R\)の座標は

\(Q(\cos \beta , \sin \beta),R(\cos \alpha ,- \sin \alpha)\)である。

\(QR\)間の距離を求めると、

\begin{eqnarray}
RQ^{2}&=&(\cos \beta - \cos \alpha)^{2}+(\sin \beta + \sin \alpha)^{2}\\
&=&2-2(\cos \alpha \cos \beta - \sin \alpha \sin \beta)
\end{eqnarray}

\(\angle AOP =\angle ROQ\)より、\(AP^{2}=RQ^{2}\)なので

\[2-2\cos (\alpha + \beta)=2-2(\cos \alpha \cos \beta - \sin \alpha \sin \beta)\]

ゆえに、

\[2\cos (\alpha + \beta)=2(\cos \alpha \cos \beta - \sin \alpha \sin \beta)\]

したがって、

\[\cos(\alpha + \beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta\]

シータ

どちらの証明も知っておいて損はないよ！

その他の加法定理の証明

\(\cos (\alpha + \beta)\)や\(\cos (\alpha - \beta)\)の加法定理を示せば、その他の加法定理も証明できます。

\begin{eqnarray}
\cos (\alpha-\beta)&=&\cos \{\alpha+(-\beta)\} \\
&=&\cos \alpha \cos (-\beta)-\sin \alpha \sin (-\beta)\\
&=&\cos \alpha \cos \beta+\sin \alpha \sin \beta\\
\end{eqnarray}

\begin{eqnarray}
\sin (\alpha+\beta)&=&\cos \{90-(\alpha+\beta)\}\\
&=&\cos \{(90-\alpha)-\beta\} \\
&=&\cos (90-\alpha) \cos \beta+\sin (90-\alpha) \sin \beta \\
&=&\sin \alpha \cos \beta+\cos \alpha \sin \beta
\end{eqnarray}

\begin{eqnarray}
\sin (\alpha-\beta)&=&\sin \{\alpha+(-\beta)\} \\
&=&\sin \alpha \cos (-\beta)+\cos \alpha \sin (-\beta) \\
&=&\sin \alpha \cos \beta-\cos \alpha \sin \beta
\end{eqnarray}

\begin{eqnarray}
\displaystyle \tan (\alpha+\beta)&=&\frac{\sin (\alpha+\beta)}{\cos (\alpha+\beta)} \\
\displaystyle &=&\frac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta }
\end{eqnarray}

分子, 分母を \(\cos \alpha \cos \beta\)で割って、

\begin{eqnarray}
\displaystyle 　&=&\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}
\end{eqnarray}
\begin{eqnarray}
\displaystyle \tan (\alpha-\beta)&=&\frac{\sin (\alpha-\beta)}{\cos (\alpha-\beta)} \\
\displaystyle &=&\frac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta+\sin \alpha \sin \beta}
\end{eqnarray}

分子, 分母を\(\cos \alpha \cos \beta \)で割って、

\begin{eqnarray}
\displaystyle 　&=&\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}
\end{eqnarray}

これですべての加法定理を証明することができました。

まずは\(\cos\)の加法定理を示すことを覚えておきましょう。