数学Ⅰデータの分析で欠かせないのが『ヒストグラム』です。
今回解決する悩み
「ヒストグラムってなんだっけ」
「ヒストグラムから中央値を求めたい」
今回はデータの中でもヒストグラムに関するこんな悩みを解決します。

今回のテーマは『ヒストグラム』です。
ヒストグラムとはデータを階級ごとの棒グラフにしたもの。
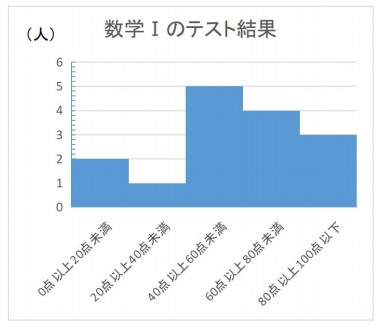
参考
階級:データを分ける区間。上のヒストグラムでは20点ごとの区間を階級と呼びます。
度数:その階級に含まれるデータの個数を表します。
グラフの用語について詳しくを知りたい方は「度数分布表の意味と各値の求め方」にて解説しています。
度数分布表の意味と各値の求め方
-

度数分布表とは?平均値・最頻値の求め方を解説!
続きを見る

ヒストグラムは読み方と書き方を理解できればとても簡単なものです。
本記事では、ヒストグラムについて解説しているので、ぜひ最後までご覧ください。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
ヒストグラムとは?
ヒストグラムとは「データを階級ごとに表した棒グラフ」です。
言葉で言われてもピンとこないと思うので例を見ていきましょう。
ここにテスト結果がありますが、これでは点数の分布がいまいち分かりません。
テスト結果
82 63 91 46 53 7 37 97 15 44 66 74 59 53 62 (点)
そこでテストの点数を20点ごとに区分けして、その様子をヒストグラムにしました。

ヒストグラムにすることで全体の分布が分かりやすくなります。
このグラフから分かること
- 40~60点の生徒が多い
- 20~40点の生徒は少ない
- 平均点は50点以上になりそう など
ヒストグラムの用語解説
ヒストグラムを読むために必要な用語の解説をします。

ヒストグラムの横軸は階級を示しています。
このヒストグラムでは、「0点以上20点未満」のように20点ごとに階級を分けしました。
このように階級が20点ごと分けてあるとき、階級の幅は20点となります。
ヒストグラムの縦軸は度数を示します。
つまり、その階級に属しているデータの数です。
横軸と縦軸をあわせて読むことで、どのくらいの点数の人が何人いるのかが分かります。
ヒストグラムと度数分布表
ヒストグラムの書き方の前に、ヒストグラムと度数分布表の関係をまとめておきます。
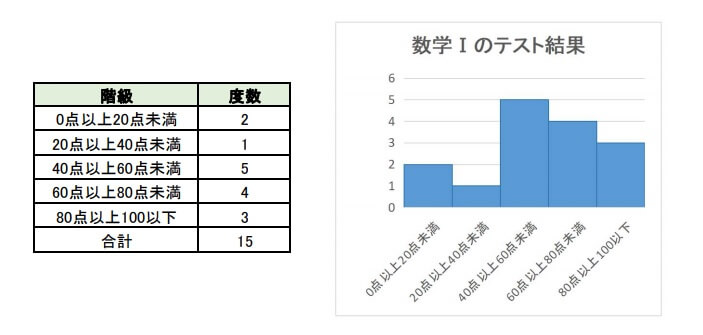
データの分布を区分けた表を度数分布表といい、それを棒グラフにしたものをヒストグラムといいます。
度数分布表からヒストグラムを書くこともありますし、その逆もあります。
ヒストグラムと度数分布表は合わせて覚えておきましょう。
-

度数分布表とは?平均値・最頻値の求め方を解説!
続きを見る
ヒストグラムの書き方
それではヒストグラムの書き方を解説します。
ここに英語のテスト結果があります。
テスト結果
82 63 91 46 53 7 37 35 26 44 66 74 59 53 38 (点)
このままでは各階級の度数が分かりづらいので、度数分布表にまとめます。
度数分布表で表したものが下の表です。
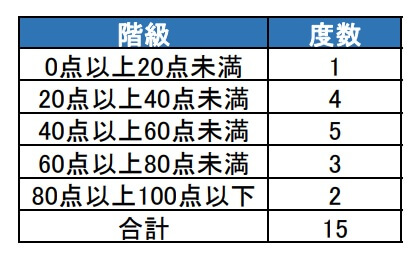
データの整理ができたのでヒストグラムを書いていきます。
横軸には階級を書き入れます。
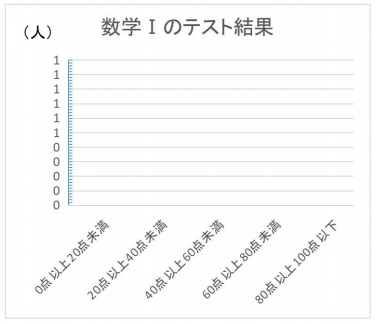
そして各階級の度数を棒グラフに表します。
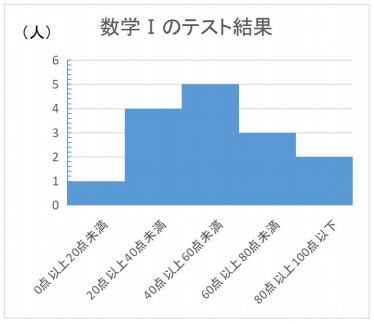
これでヒストグラムの完成です。


いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。

ヒストグラムから平均値を求める
ここからはヒストグラムを用いた各値の求め方を解説していきます。
まずはヒストグラムから平均値を求める方法です。
このような問題が出題されることがあります。
問題

ヒストグラムから平均値を求める手順は以下の通りです。
平均値を求める手順
- 度数分布表で表す
- 階級値を求める
- 階級値×度数を求める
- 平均値を求める
1.度数分布表で表す
ヒストグラムから平均値を求めるには、まず度数分布表に直します。
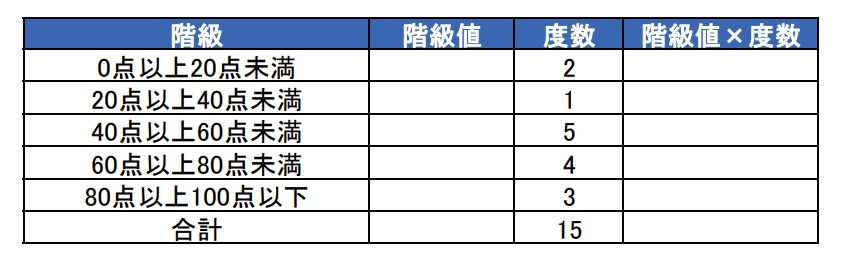
2.階級値を求める
次に各階級の階級値を求めます。
階級値とは各階級の中央値を指します。
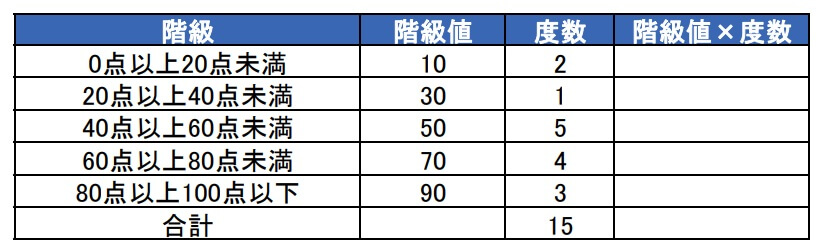
3.階級値×度数を求める
そして、各階級の階級値と度数の積を求めます。
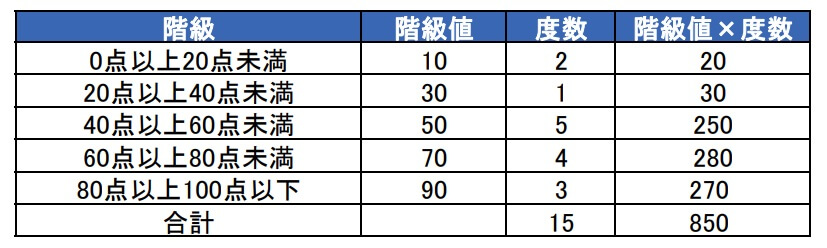
4.平均値を求める
3で求めた「階級値×度数」を度数の合計で割ったものがヒストグラムの平均値です。
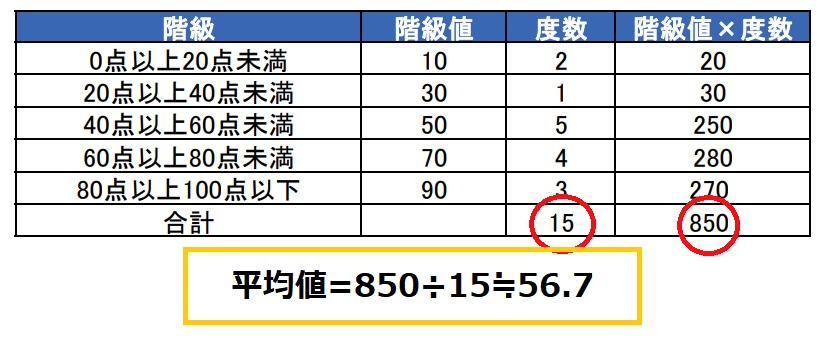
したがって、求める平均値は56.7点ということが分かりました。
ヒストグラムの平均値とデータの平均値は求め方が大きく異なります。
もっと詳しく
データの平均値の求め方はこちら 続きを見る

平均値の求め方を解説!中央値との違いはズバリこれ!
ヒストグラムの中央値の求め方
次はヒストグラムから中央値を求める方法について解説します。
このヒストグラムにはデータが15個あります。
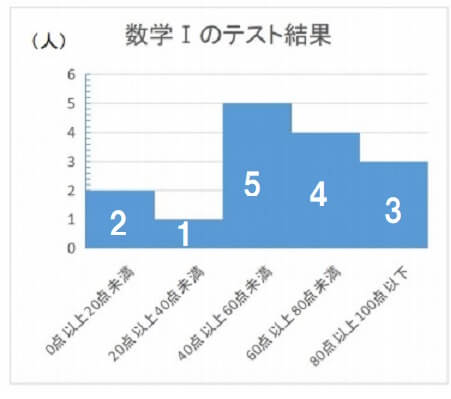
つまり、求めたい中央値は小さい順に並べたときの8番目のデータです。
数えてみると8番目のデータが「40点以上60点未満」の階級に属していることが分かります。
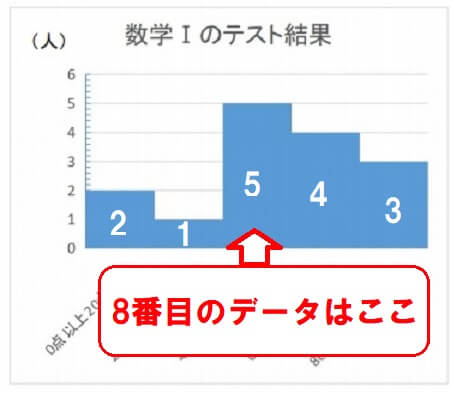
ヒストグラムの中央値は「中央のデータが属する階級の階級値」
したがって、中央値は50点となります。
データの中央値とヒストグラムの中央値は求め方が少し異なります。
データの中央値について詳しく知りたい方は「中央値の求め方とメリット」を参考にしてください。
ヒストグラム<練習問題>

ここまでヒストグラムの書き方や平均値などの求め方について解説してきました。
下のデータを読み取りヒストグラムを作ってください。
テスト結果
83 64 96 43 52 9 31 93 18 46 63 77 51 57 64 (点)
まずは度数分布表にします。
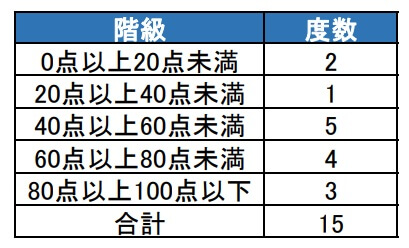
ここから各階級の度数を読み取りグラフにします。
解答

ヒストグラム まとめ
今回はデータの分析からヒストグラムについてまとめました。
度数分布表が作れるようになれば、ヒストグラムも簡単に作図できます。
ヒストグラムまとめ

ヒストグラム
⇒データを階級ごとに分け、その分布を表した棒グラフ
ヒストグラムはすぐに得点アップに繋がるのでこの機会にしっかり理解しておきましょう。
データの分析には重要な公式がたくさんあります。
分散や相関係数についても別記事でまとめているので合わせてご覧ください。
他にもデータの分析に関する悩みがある方は「データの分析まとめ記事」をご覧ください。
-

【数学Ⅰ】データの分析重要公式まとめ《完全攻略》
続きを見る
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。








