今回解決する悩み
「等しいベクトルとは？」
「ベクトルの大きさって？」
ベクトルの”大きさ"とは長さを表しています。
大きさの求め方は簡単なので必ず押さえておきましょう。
本記事では、ベクトルの大きさを求める公式を解説しています。
ベクトルの大きさと求め方
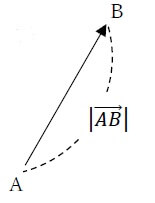
下図のような大きさと向きで定まるものをベクトルといいます。
有向線分ABで表されるベクトルを、\(\overrightarrow{ AB }\)と書き表す。
このとき、線分ABの長さをベクトルABの"大きさ"として\(|\overrightarrow{ AB }|\)と表します。
平面ベクトルのとき
平面ベクトルの大きさの求め方を紹介します。
\(\vec{AB} = (x, y)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2}\]
\(A(0,0),B(3,4)\)とすると\(\vec{AB} = (3, 4)\)の大きさは、
\[|\overrightarrow{ AB }|=\sqrt{3^2 + 4^2}=\sqrt{25}=5\]
したがって、\(\vec{AB} = (3, 4)\)の大きさは5ということが分かりました。
空間ベクトルのとき
空間ベクトルの場合は成分が3つになるので、大きさの求め方も変わります。
\(\vec{AB} = (x, y, z)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2 +z^2}\]
\(A(0,0,0),B(3,4,5)\)とすると\(\vec{AB} = (3, 4,5)\)の大きさは、
\[|\overrightarrow{ AB }|=\sqrt{3^2 + 4^2 +5^2}=\sqrt{50}=5\sqrt{2}\]
したがって、\(\vec{AB} = (3, 4 ,5)\)の大きさは\(5\sqrt{2}\)ということが分かりました。
単位ベクトルは大きさ1
単位ベクトルとは、大きさが１のベクトルです。
単位ベクトルの具体例を見てみましょう。
\(\displaystyle A(0,0),B(\frac{3}{5},\frac{4}{5})\)とすると\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)です。
このとき\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)の大きさは、
\[\displaystyle |\overrightarrow{ AB }|=\sqrt{(\frac{3}{5})^2 + (\frac{4}{5})^2}=\sqrt{\frac{9}{25} + \frac{16}{25}}=1\]
したがって、\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)は大きさが1なので単位ベクトルです。
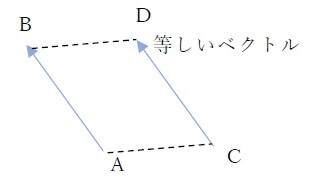
大きさの等しいベクトルとは？
\(\vec{a}と\vec{b}\)の向きと大きさが等しいとき、
２つのベクトルは等しいといい、\(\vec{a}＝\vec{b}\)と書く。
大きさも向きも等しいので、等しい2つのベクトルは平行移動するとぴったりと重ねることができます。
なぜベクトルの大きさは2乗？
ベクトルの大きさは先に2乗して、あとから2乗を外す求め方もあります。
\(A(0,0),B(3,4)\)とすると
\[|\overrightarrow{ AB }|^{2}=3^2 + 4^2=25\]
\(|\overrightarrow{ AB }| \ge 0\)なので、
\[|\overrightarrow{ AB }|=5\]
先ほど解説した公式では、ルートを使いましたがこの公式ではルートを後回しにできます。
ベクトルのおすすめ勉強法
ベクトルは受験でもよく出題されるの重要単元の1つです。
問題の意図をしっかり理解して、自分で応用できる力が必要です。
次はベクトルに関する問題のおすすめ勉強法を紹介します。
- 教科書やノートを見直す
- 問題集で応用力を磨く
- 分かりやすい解説を見る
自分のいまの理解度と目標を照らし合わせて、自分に合った勉強法を試してみてください。
教科書やノートを見直す
まずは基本に立ち返って、教科書・ノートを見直してみましょう。
教科書には重要なポイントがギュッと詰まっています。
まず公式が覚えられていないと応用もできないので、まずは教科書問題を完璧にしましょう。
問題集で応用力を磨く
ベクトルに慣れてきたら問題のレベルを上げて応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
ベクトルの学習におすすめの問題集を紹介します。
《教科書レベル》
《入試準備レベル》
《網羅型》
Amazon会員なら参考書も読み放題です。
初回30日間の無料体験あり。
⇒参考書が読み放題！Kindle Unlimitedについて詳しく知りたい
分かりやすい解説を見る
以下のような悩みがあるなら映像授業もおすすめです。
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
映像授業なら自分に必要な授業のみを受けられるうえに、分かるまで繰り返し視聴することができます。
分からないを1つずつ解消していけるので、定期テストで高得点を取りたい方は授業授業がおすすめです。
映像授業で学ぶメリット
映像授業で学ぶことのメリットを3つ紹介します。
映像授業で学ぶメリット
- 勉強に対する苦手意識がなくなる
- 目標に最短ルートで近づける
- 楽しい高校生活と勉強の両立
勉強に対する苦手意識がなくなる
映像授業では各教科のプロが授業をするので、かなり分かりやすい解説が多いです。
高校生のつまづきやすいポイントをしっかりと押さえた分かりやすい授業で、苦手単元を1つずつ解消していきます。
目標に最短ルートで近づける
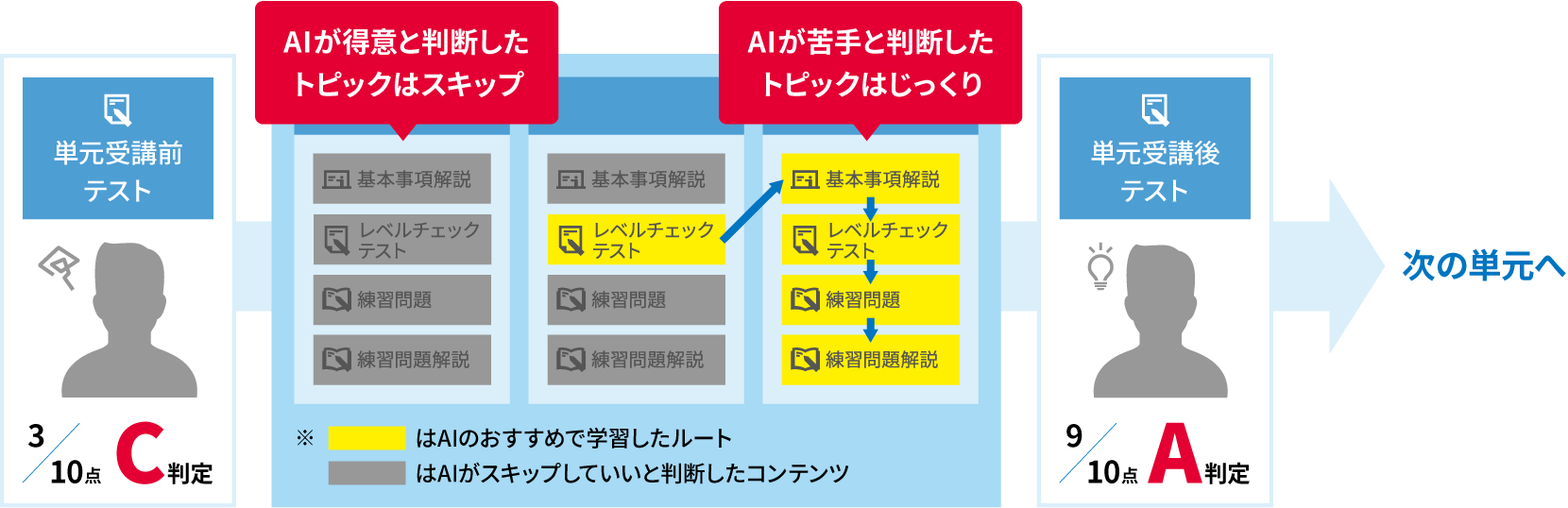
河合塾Oneの「自分専用カリキュラム」
自分に必要な授業だけを受けられるので、最短ルートで目標に近づきます。
ただひたすらに解説を写すような勉強は時間がもったいないです。
自分のレベルに合わせた授業だけを受けて、最短で目標達成を目指します。
楽しい高校生活と勉強の両立
1回の授業が15分程度で、ネット環境があればどこからでも受講できます。
通学の電車でもサクッと復習できるので、部活や遊びとの両立も可能です。
目的に合わせて選ぶことが重要
映像授業といっても様々なサービスがあります。
どこでも良いわけではなく、あなたの目標に合った映像授業を選ぶことが重要です。
| サービス名 | こんな方におすすめ |
| 河合塾One | 定期テスト対策がしたい |
| スタディサプリ | 受験に向けて勉強したい |
| 進研ゼミ | テキストも欲しい |
"河合塾One"と"スタディサプリ"には無料体験があります。
どちらも会員数をグングン伸ばしているので、いつ無料体験がなくなるか分かりません。
ちなみに、定期テスト対策なら「河合塾One」、受験に向けて始めるなら「スタディサプリ」がおすすめです。
無料体験期間
定期テストに向けて無料体験の期間で総復習するのもオススメです！
高校生向けの映像授業をランキング形式でまとめました。
ベクトルの大きさ まとめ
今回はベクトルの大きさについてまとめました。
ベクトル大きさ平面ベクトルの大きさの求め方
\(\vec{AB} = (x, y)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2}\]
空間ベクトルの大きさの求め方
\(\vec{AB} = (x, y, z)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2 +z^2}\]
ベクトルが苦手な方は多いと思いますが、慣れるまでは矢印だと思えば良いです。
まずは公式をしっかりと覚えてからが勝負です。
ベクトル以外の単元についてもまとめ記事を出しています。
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
ぼくがたった4ヶ月で偏差値を19上げることができた体験談はこちら
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように！
マストラ公式LINEアカウントを友達登録しよう！
マストラのLINE公式アカウントができました！
～実際の公式LINEのメニュー～
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ！
高校生向けの様々なコンテンツを配信予定！
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね！
▼この機会にぜひ登録！
完全個別指導のスタディトレーナー
スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服！
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応！
無料体験授業から始められるので、お気軽に申し込み下さい。
![Pinterest](https://www.pinterest.com/pin/create/button/?url=https%3A%2F%2Fmath-travel.com%2Fhighb1-1-1%2F&media=https://math-travel.com/wp-content/uploads/2020/03/ベクトル.png&description=今回解決する悩み 「等しいベクトルとは？」 「ベクトルの大きさって？」 ベクトルの”大きさ"とは長さを表しています。 大きさの求め方は簡単なので必ず押さえておきましょう。 本記){kind=link}