「なんで半角の公式は成り立つの?」
「すぐ忘れるので導き方を知りたい」
今回は半角の公式に関するこんな悩みを解決します。

半角の公式は三角関数の重要な公式の1つです。
半角の公式
\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}
半角の公式は、\(\displaystyle \sin^{2} \frac{\theta}{2}\)のような、\(\displaystyle \frac{\theta}{2}\)の三角比を求める公式です。
本記事では半角の公式の証明や導き方を解説しています。
公式の作り方が分かるようになるので、ぜひ最後までご覧ください。。
記事の内容
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
半角の公式 証明
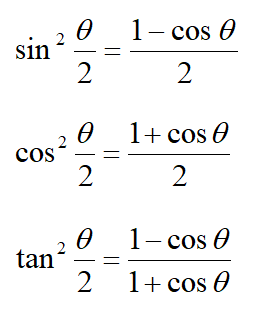
半角の公式は2倍角の公式を活用して証明します。
1つずつ証明していきましょう。
- \(\sin\)の半角公式
- \(\cos\)の半角公式
- \(\tan\)の半角公式

\(\sin\)の半角の公式 証明
まずは\(\sin\)の半角の公式を証明します。
半角の公式の証明には2倍角の公式を使います。
2倍角の公式
\begin{eqnarray}
\cos 2\theta&=&\cos^{2} \theta-\sin^{2} \theta\\
&=&1-2\sin^{2} \theta \\
&=&2 \cos^{2} \theta -1
\end{eqnarray}
2倍角の公式より、
\[\cos 2\theta=1-2\sin^{2} \theta\]
ここで\(\theta\)を\(\displaystyle \frac{\theta}{2}\)に置き換えると、
\[\displaystyle \cos 2 \cdot \frac{\theta}{2}=1-2\sin^{2} \frac{\theta}{2}\]
よって、
\[\displaystyle \cos \theta=1−2 \sin^{2} \frac{\theta}{2}\]
式を整理することで、
\[\displaystyle \sin^{2} \frac{\theta}{2}=\frac{1-\cos \theta}{2}\]
証明終了。
\(\cos\)の半角の公式 証明
同様に2倍角の公式より
\[\cos 2\theta=2\cos^{2} \theta -1\]
\(\sin\)と同様に\(\theta\)を\(\displaystyle \frac{\theta}{2}\)に置き換えて、
\[\displaystyle \cos 2 \cdot \frac{\theta}{2}=2\cos^{2} \frac{\theta}{2}-1\]
よって、
\[\displaystyle \cos \theta=2 \cos^{2} \frac{\theta}{2}-1\]
式を整理することで、
\[\displaystyle \cos^{2} \frac{\theta}{2}=\frac{1+\cos \theta}{2}\]
証明終了。
\(\tan\)の半角の公式 証明
\(\tan\)の半角の公式は
\[\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\]
を用いると簡単に証明ができます。
\begin{eqnarray}
\displaystyle \tan^{2} \frac{\theta}{2}&=&\frac{\sin^{2} \frac{\theta}{2}}{\cos^{2} \frac{\theta}{2}}\\
\displaystyle &=&\frac{\frac{1-\cos \theta}{2}}{\frac{1+\cos \theta}{2}}\\
\displaystyle &=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}
これで半角の公式を証明することができました。
ポイントは加法定理からの式変形です。
2倍角の公式についてはこちらの記事で詳しく解説しました。
-

2倍角の公式と求め方!cosの変形をマスターしよう!

半角の公式の導き方
「半角の公式は複雑なので、よく忘れてしまいます...」
そんなときに私がやっている半角の公式の導き方を紹介します。
半角の公式を導く
- 加法定理を思い出す
- 式変形をする
- 数字を代入する
以下の問題を例として導いてみましょう。
例題
次の値を求めてみよう。
\[\displaystyle \sin^{2} \frac{\pi}{8}\]
\(\displaystyle \frac{\pi}{8}\)なので半角の公式を使いたいですが、公式を忘れてしまったとしましょう。
step
1加法定理を思い出す
まず\(\cos\)の加法定理を書きます。
\[\cos 2\theta=\cos^{2}\theta-\sin^{2}\theta\]
今回は\(\displaystyle \sin \frac{\pi}{8}\)を求めたいので、
\[\cos 2\theta=1-2\sin^{2}\theta \cdots ①\]
を導きます。
step
2式変形をする
①を整理すると、
\[2\sin^{2}\theta=1-\cos 2\theta\]
式変形して、
\[\displaystyle \sin^{2} \theta=\frac{1-\cos 2 \theta}{2} \cdots ②\]
step
3数字を代入する
②の\(\theta\)に\(\displaystyle \frac{\pi}{8}\)を代入します。
\begin{eqnarray}
\displaystyle \sin^{2} \frac{\pi}{8}&=&\frac{1-\cos \frac{\pi}{4}}{2}\\
\displaystyle &=&\frac{1-\frac{\sqrt{2}}{2}}{2}\\
\end{eqnarray}
したがって、
\[\displaystyle \sin^{2} \frac{\pi}{8}=\frac{2-\sqrt{2}}{4}\]
この手順なら半角の公式を忘れても、公式を作ることができます。
半角の公式の覚え方が知りたい方はこちら

半角の公式<練習問題>
半角の公式を使って練習問題にチャレンジしてみましょう。
練習問題
\(\displaystyle \frac{\pi}{2}<\theta<\pi\)で\(\displaystyle \sin \theta=\frac{3}{5}\)のとき、\(\displaystyle \sin \frac{\theta}{2}\)の值を求めよ。
半角の公式を使うために、\(\cos \theta \)から求めましょう。
三角形の相互関係より、
\[\sin^{2}\theta +\cos^{2} \theta=1\]
なので、
\begin{eqnarray}
\cos^{2} \theta&=&1-\sin^{2} \theta\\
\displaystyle &=&1-(\frac{3}{5})^{2}\\
\displaystyle &=&\frac{16}{25}
\end{eqnarray}
\(\displaystyle \frac{\pi}{2} < \theta < \pi \)のとき、\(cos \theta < 0 \)なので、
\[\displaystyle cos \theta =-\frac{4}{5}\]
よって、sin の半角の公式を用いると
\begin{eqnarray}
\displaystyle \sin ^{2} \frac{\theta}{2} &=& \frac{1-\cos \theta}{2}\\
\displaystyle &=&\frac{1-(-\frac{4}{5})}{2}\\
\displaystyle &=&\frac{\frac{9}{5}}{2}\\
\displaystyle &=&\frac{9}{10}
\end{eqnarray}
\(\displaystyle \frac{\pi}{2}<\theta<{\pi}\)より、\(\displaystyle \frac{\pi}{4}<\frac{\theta}{2}<\frac{\pi}{2}\)であるから、
ゆえに、\(\displaystyle \sin \frac{\theta}{2}>0\)である。
したがって、
\[\displaystyle \sin \frac{\theta}{2}=\frac{3\sqrt{10}}{10}\]
となります。

半角の公式の証明 まとめ
今回は半角の公式の証明についてまとめました。
半角の公式 証明半角の公式
\begin{eqnarray}
\displaystyle \sin^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{2}\\
\displaystyle \cos ^{2} \frac{\theta}{2}&=&\frac{1+\cos \theta}{2}\\
\displaystyle \tan ^{2} \frac{\theta}{2}&=&\frac{1-\cos \theta}{1+\cos \theta}
\end{eqnarray}
証明のポイント
2倍角の公式を活用して証明する。
\begin{eqnarray}
\cos 2\theta&=&\cos^{2}-\sin^{2}\\
&=&1-2\sin^{2}\\
&=&2\cos^{2}-1
\end{eqnarray}
半角の公式を忘れたときは以下の手順で導きましょう。
半角の公式を導く
- 加法定理を思い出す
- 式変形をする
- 数字を代入する
今回は半角の公式の証明を中心に解説してきました。
半角の公式や使い方が知りたい方はこちらの記事がおすすめです。
-

半角の公式の覚え方や使い方を徹底解説!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。








