数学Ⅰの二次関数において「判別式D」は重要な公式です。
今回解決する悩み
「判別式Dとは?」
「実数解や共有点の個数を求めたい」
本記事では2次関数に欠かせない判別式Dについて解説します。

高校数学において、判別式Dは非常に重要な公式の1つです。
判別式Dを求める公式は以下の通りです。
判別式Dの公式
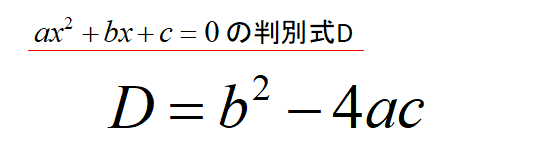
判別式Dを利用することで、二次方程式の実数解の個数が分かります。

本記事では、判別式Dの公式と解の個数との関係について解説します。
段階を踏んで解説するので、ぜひ読んでみてください。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
判別式Dとは?
まず判別式Dとは以下の公式を指しています。
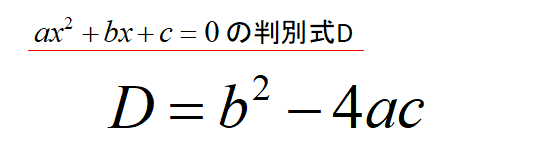
《判別式Dの公式》
二次方程式における各項の係数を\(a,b,c\)として、
判別式Dの公式
\(y=ax^2+bx+c\)のとき判別式\(D\)は
\[D=b^{2}-4ac\]
各値を\(a,b,c\)に代入することで、Dの値を求めます。
この判別式Dの符号によって、二次方程式が実数解をいくつ持つのかを判断することができます。

判別式Dと実数解の個数
判別式Dの符号によって実数解の個数が分かると書きましたが、もう少し深掘りして解説します。

判別式Dと解の個数
D>0のとき、異なる実数解を2つもつ。
D=のとき、実数解を1つもつ。(重解)
D<0のとき、実数解をもたない。
言葉だけではピンとこないと思うので、実際に数字を入れて考えてみましょう。
2次方程式\(x^{2}+2x-3=0\)の実数解の個数を求めよう。
解答
2次方程式\(x^{2}+2x-3=0\)の判別式をDとすると
\[D=2^{2}-4 \cdot 1 \cdot (-3)=16>0\]
\(D>0\)なので、実数解の個数は2個である。

公式LINEから簡単なアンケートに答えるだけで、『2次関数』の重要公式をまとめたPDFをプレゼント中です!

判別式Dと共有点の個数
判別式Dの符号によって、2次関数とx軸との共有点の個数が分かります。
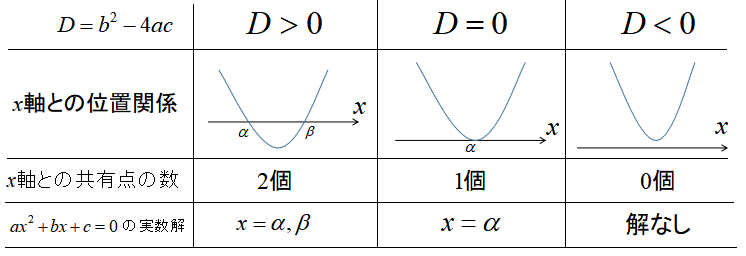
つまり、判別式Dの符号によって以下の3つのことがいえます。
判別式Dとx軸との関係
①D>0のとき、二次方程式は異なる2つに実数解をもつので、x軸と2か所で交わる。

②D=0のとき、二次方程式は1つの実数解をもつので、x軸と接している。

③D<0のとき、二次方程式は実数解をもたないのでx軸とは交わらない。


そもそも\(ax^{2}+bx+c=0\)というのは、
\(y=ax^{2}+bx+c\)とx軸の交点のx座標を求めています。
どういうことかと言うと
2次方程式\(x^{2}-6x+8=0\)を例として
\begin{eqnarray}
x^{2}-6x+8&=&0\\
(x-2)(x-4)&=&0\\
x&=&2,4
\end{eqnarray}
となりますが、
これは2次関数\(y=x^{2}-6x+8\)が\(x=2,4\)でx軸と交わることを表しています。
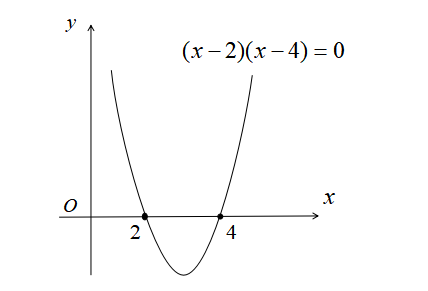
2次方程式の解が何を表しているのか、しっかり理解している学生は少ないでしょう。
上図のように、2次関数とx軸が2点で交わる状態を「異なる2つの実数解をもつ」といいます。
判別式Dを用いた練習問題
2次関数の分野で判別式Dを使った練習問題に挑戦してみましょう。
2次方程式の実数解の個数

解答
(1) \(a=1,b=-4,c=5\)として、判別式Dの符号を求めます。
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&(-4)^{2}-4 \cdot 1 \cdot 5\\
&=&16-20\\
&=&-4<0
\end{eqnarray}
したがって、実数解をもたない。
条件を満たす\(m\)の範囲

解答
(1) \(a=1,b=5,c=m\)として、判別式Dの符号を求める。
\begin{eqnarray}
D&=&b^{2}-4ac\\
&=&5^{2}-4 \cdot 1 \cdot m\\
&=&25-4m
\end{eqnarray}
与式が異なる2つの実数解をもつためには、\(D>0\)であればよい。
ゆえに、
\begin{eqnarray}
25-4m&>&0\\
4m&<&25\\
m&<&\frac{25}{4}
\end{eqnarray}
したがって、求める範囲は\(m< \dfrac{25}{4}\)
2次関数とx軸の共有点の個数

解答
(1) \(y=x^{2}-3x+1\)について
\begin{eqnarray}
D&=&(-3)^{2}-4 \cdot 1 \cdot 1\\
&=&9-4\\
&=&5>0
\end{eqnarray}
よって、共有点の個数は2個
判別式Dと解の公式を使い方の違い
判別式Dと解の公式はどちらも2次関数では欠かせない公式です。
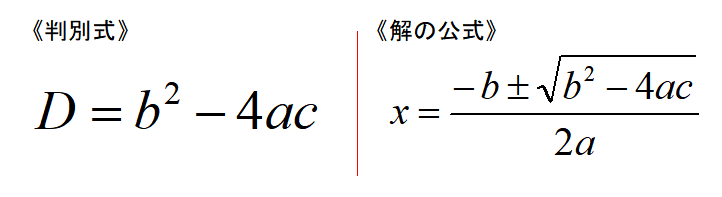
しかし、それぞれの使い方は明確に異なります。
「実数解がいくつあるのか」「共有点がいくつあるのか」といった、解の個数が分かれば良い問題に判別式Dを使います。
判別式では解の個数は分かりますが、具体的なx座標の値までは分かりません。
一方で、解の公式は判別式よりも強力です。
解の公式を使うことで、2次方程式の解まで分かります。
つまり、判別式Dと解の公式を使うときの違いは
判別式Dと解の公式の使い分け
- 実数解の個数が知りたいなら⇒判別式D
- 2次方程式の解を求めたいなら⇒解の公式
なぜ解の個数が分かるの?

そんなギモンの声が聞こえてきそうなので、なぜ判別式Dで実数解の個数が分かるのかを解説します。
まず、判別式Dの公式は以下の数式でしたね。
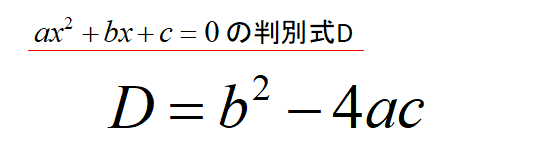
\(b^{2}-4ac\)ってどこかで見たことがある形をしていませんか?
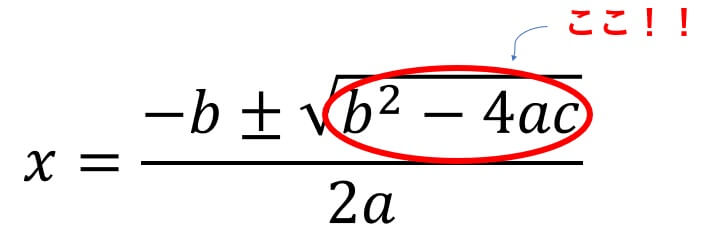
そうです、判別式Dは解の公式のこの部分と同じ形をしているのです!
つまり、Dの符号によって以下の3パターンに分けて考えることができます。
\(D>0\)のとき
\(D>0\)のとき、解の公式におけるルート部分が正の数になることを表します。
つまり、二次方程式を満たす解が2つあることを指します。
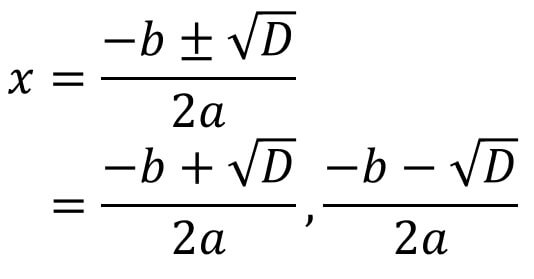
このことから、D>0のとき二次方程式が2つの実数解をもつことが分かります。
\(D=0\)のとき
\(D=0\)のとき、解の公式におけるルートの部分が\(b^{2}-4ac=0\)ですね。
これは二次方程式を満たす解が1つしかないことを指します。
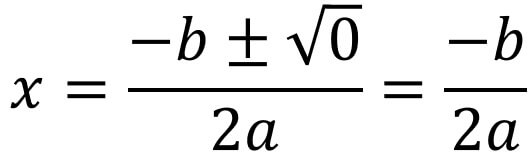
したがって、D=0のとき二次方程式は実数解を1つもつことが分かりました。
\(D<0\)のとき
\(D<0\)のとき、解の公式におけるルート部分の中身がマイナスになってしまいます。
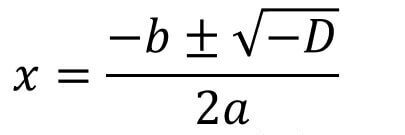
数学Ⅰの段階ではルートの中身が正の数でなければならないため、\(D<0\)のとき\(x\)は実数解を持たないのです。
これは余談ですが、数Ⅱではルートの中が負の数になることがあり、「虚数」と呼ばれる単元に繋がっていきます。
>>実数とは?実数に含まれるもの&実数でないものを具体例で解説
参考
そもそも解の公式について知りたい方は以下の記事がおすすめ
⇒二次方程式の解の公式をマスターしよう!
判別式D/4を活用しよう
判別式Dを少し応用したもので、\(\displaystyle \frac{D}{4}\)というものがあります。
\(\displaystyle \frac{D}{4}\)は与えられた二次方程式\(ax^{2}+bx+c=0\)の\(b\)が偶数のときにだけ使える公式です。
判別式D/4
\(y=ax^{2}+bx+c\)において、\(b\)が偶数のとき\(\displaystyle b'=\frac{b}{2}\)とすると
\[\displaystyle \frac{D}{4}=b'^{2}-ac\]
例として、二次方程式\(x^{2}+6x+3=0\)の解の個数を求めましょう。
\(x\)の係数が\(6\)で偶数なので、判別式\(\displaystyle \frac{D}{4}\)を使うことができます。
\(b'=3\)とすると、
\begin{eqnarray}
\frac{D}{4}&=&b'^{2}-ac\\
&=&3^{2}-1 \cdot 3\\
&=&6
\end{eqnarray}
\(\displaystyle \frac{D}{4}>0\)より、与えられた二次方程式は異なる2つの実数解をもつ。

なんで判別式はDなの?
ここで少し余談なのですが、「なぜ判別式の記号はDなのでしょうか」。
それにはちゃんとした由来があります。

Dは英語の略称で英単語の「discriminant」(日本語訳:判別、差別、区別)が由来になっています。
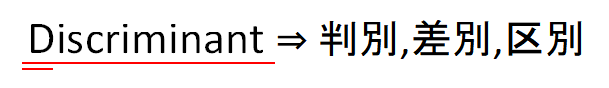
何気なく使っている数学の記号にはちゃんと意味があるので、そこを気にしてみても面白いですね!
2次関数のおすすめ勉強法

2次関数は数学Ⅰのなかでも、解きやすい問題が多い単元です。
問題の意図をしっかり理解できれば、解法もすぐに思いつくようになります。
さて、ここでは2次関数のおすすめ勉強法を紹介します。
- 教科書やノートを見直す
- 問題集で応用力を磨く
- 分かりやすい解説を見る
あなたの理解度に合わせて、自分に合った勉強法を試してみてください。

教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。
教科書には重要なポイントがギュッと詰まっています。
マストラでも2次関数の基本については「2次関数の公式まとめ」にて解説しているのでご覧ください。

問題集で応用力を磨く

2次関数の関する公式に慣れてきたら、次は問題を解いて応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
2次関数の学習におすすめの問題集を紹介します。
Amazon会員なら参考書も読み放題です。
初回30日間の無料体験あり。
⇒参考書が読み放題!Kindle Unlimitedについて詳しく知りたい
分かりやすい解説を見る
以下のような悩みがあるなら映像授業もおすすめです。
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
映像授業なら自分に必要な授業のみを受けられるうえに、分かるまで繰り返し視聴することができます。
分からないを1つずつ解消していけるので、定期テストで高得点を取りたい方は授業授業がおすすめです。
判別式Dの公式 まとめ
今回は二次方程式の判別式についてまとめました。
二次方程式の判別式 まとめ判別式D

判別式Dとx軸との共有点の個数

判別式Dは重要な公式です。なので、必ず押さえておきましょう!
また、判別式Dの符号によって解の個数が定まる理由も覚えておくことで、より理解が深まります。
\(x\)軸との共有点の個数は、2次関数の頂点の位置からも判断できます。
2次関数の軸と頂点については「2次関数の頂点・軸を求める手順」で解説しています。
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!
公式LINEから簡単なアンケートに答えるだけで、『2次関数』の重要公式をまとめたPDFをプレゼント中です!








