数学Ⅰデータの分析で欠かせないのが『度数分布表』ですよね。
今回解決する悩み
「度数分布表ってなんだっけ」
「度数分布表が読み取れない」
今回は度数分布表に関するこんな悩みを解決します。

今回のテーマは『度数分布表』ですが、度数分布表は理解すればすぐに点数が取れます。
ぼく自身も各用語の意味と求め方を理解したらすぐに点数が取れるようになりました。
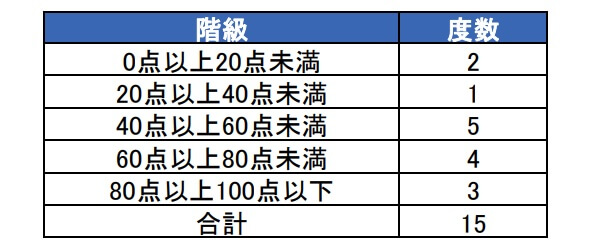
まず度数分布表とは下図のような階級ごとにデータを分けて表にしたものです。
データが下のようにバラバラに表されているとデータ全体の分布が分かりづらいですよね。
テスト結果
82 63 91 46 53 7 37 97 15 44 66 74 59 53 62 (点)
しかし、度数分布表を使うことでどの階級にデータが多いのかが一目瞭然です。
本記事では度数分布表の意味と各値の求め方を解説します。
目次
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
度数分布表とは?
度数分布表とは「データを階級ごとに分けて分布を表した表」です。
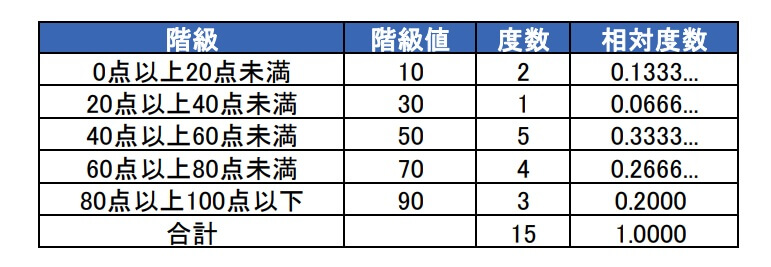

では実際に度数分布表を作ってみましょう。
ここに数学のテスト結果が15人分あります。
テスト結果
82 63 91 46 53 7 37 97 15 44 66 74 59 53 62 (点)
このままでは全体の分布がイマイチ掴めません。
そこでテストの点数を階級ごとに分けて表したものが度数分布表です。

度数分布表にしたことで20~40点の生徒が1名だけで、40~60点の生徒が5名もいることが分かりやすくなりました。


とはいえ、度数分布表の中に見慣れない言葉が多いと思います。
度数分布表の用語を確認してから各値の求め方を確認しましょう。
度数分布表の用語解説
度数分布表には、データを表す様々な言葉が入っています。
それぞれの用語の意味を解説します。
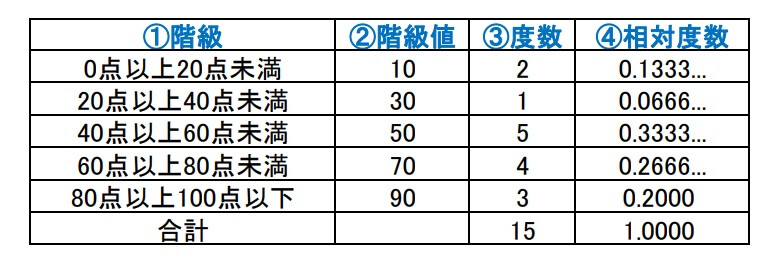
用語の解説
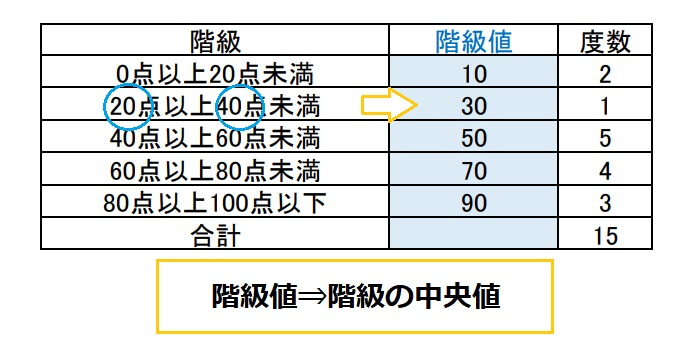
②階級値:各階級の真ん中の値を階級値といいます。たとえば「20点以上40点未満」の階級の階級値は30です。
③度数:その階級に含まれるデータの個数を表します。
④相対度数:全体の度数に対して、その階級に属する度数の割合
⑤階級の幅:階級の広さを指します。この度数分布表では20点ごとに区切っているので階級の幅は20です。
どれも確実に覚えて欲しい用語なので、上表を参考にいま覚えましょう。
度数分布表を使いこなせばデータ全体の分布が掴みやすくなります。
各値の求め方

度数分布表を用いることで平均値や中央値など、様々な値を求めることができます。
そこで度数分布表を用いた各値の求め方について確認していきましょう。
各値の求め方
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。

度数の求め方
⇒階級に当てはまるデータの個数を数える
度数とは「各階級に属するデータの個数」を指します。

たとえば上図のような度数分布表のとき、Aさんが75点ならば「60点以上80点以下」の階級に属しています。
今回は60点~80点の生徒が4人いたので、「60点以上80点以下」の度数を4とします。

階級の幅の求め方
⇒階級の最大値-最小値
階級の幅は、「階級の最大値と最小値の差」で求めます。
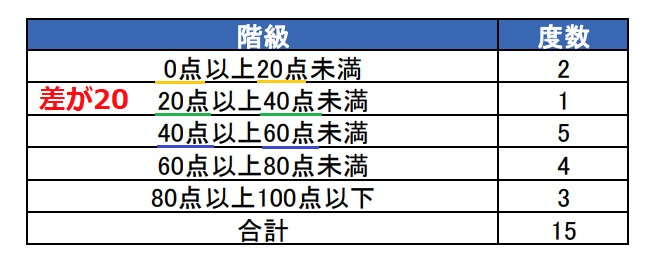
するとこの度数分布表の階級の幅は
\(60-40=20\)
他にも身長のデータの場合、「160cm以上170cm未満」の階級ならば階級の幅は10cmとなります。
階級値の求め方
⇒(階級の最大値+最小値)÷2
階級値とは「階級の中央値」を指します。
「60点以上80点以下」の階級には63点,66点,74点,62点のテスト結果が含まれています。
このとき階級値というのはデータの平均ではなく、階級の中央値を指します。
つまり、\(\displaystyle \frac{60+80}{2}=70\)となり階級値は70点です。
相対度数の求め方
⇒\(\displaystyle 相対度数=\frac{その階級の度数}{度数の合計}\)
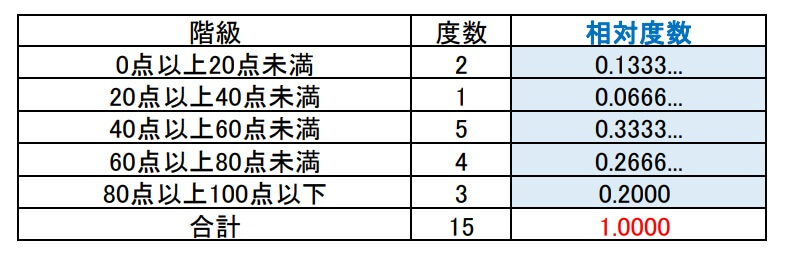
0点以上20点以下の相対度数
\(\displaystyle \frac{2}{15}=0.1333...\)
20点以上40点以下の相対度数
\(\displaystyle \frac{1}{15}=0.0666...\)
40点以上60点以下の相対度数
\(\displaystyle \frac{5}{15}=0.3333...\)
60点以上80以下の相対度数
\(\displaystyle \frac{4}{15}=0.2666...\)
80点以上100点以下の相対度数
\(\displaystyle \frac{3}{15}=0.2000\)
相対度数は割合なので相対度数の合計は1.000になります。
度数分布表の平均値
度数分布表における平均値の求め方はかなり複雑です。
平均値の求め方
- 階級値を求める
- 階級値×度数を求める
- 平均値=(2の合計)÷度数の合計
以下の度数分布表の平均値を求めていきます。
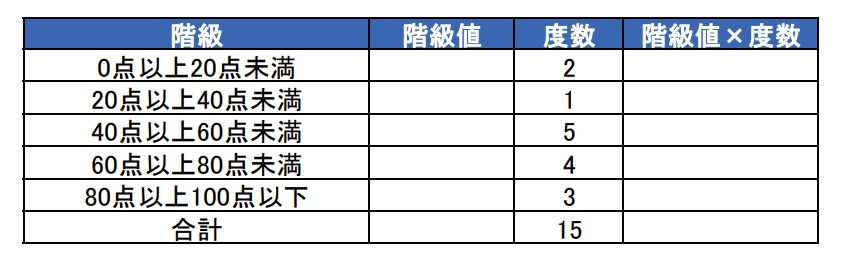
1.階級値を求める
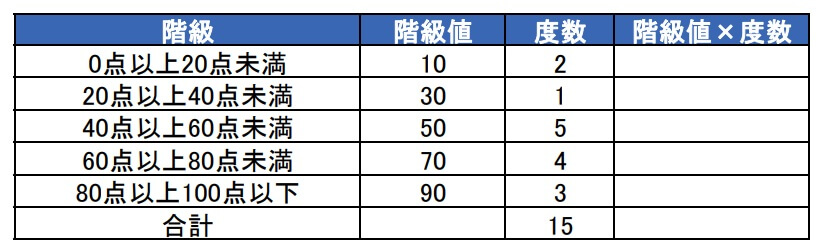
まずは各階級の階級値を求めます。
階級値は"階級の中央値"なので、\(\displaystyle \frac{階級の最大値+最小値}{2}\)で求めます。
2.階級値×度数を求める
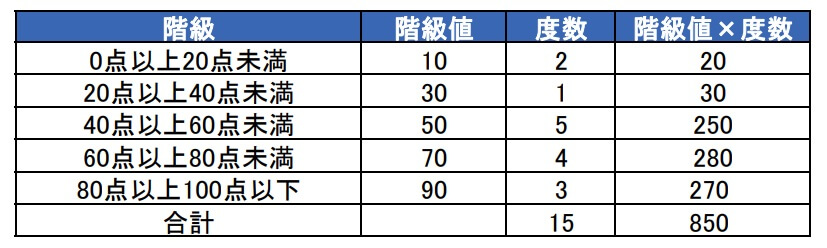
1で求めた階級値と度数の積を求めます。
3.平均値を求める
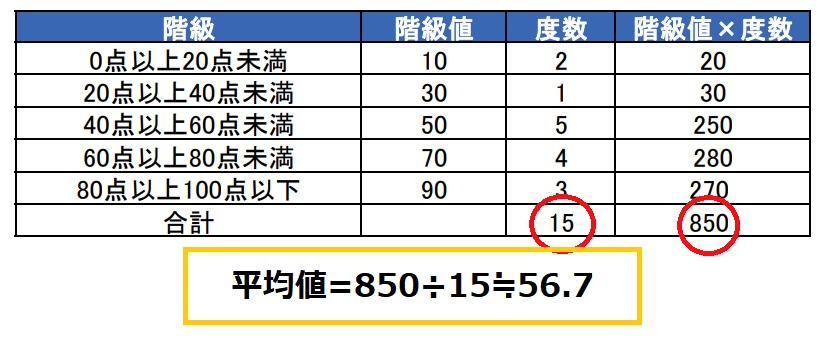
「階級値×度数」を度数の合計で割ったものが度数分布表の平均値です。
度数分布表の平均値とデータの平均値は求め方が大きく異なります。
もっと詳しく
データの平均値の求め方はこちら 続きを見る

平均値の求め方を解説!中央値との違いはズバリこれ!
度数分布表の最頻値
⇒度数が1番多い階級の階級値

この度数分布表において1番度数が多いのは「40点以上60点以下」の階級です。
最頻値というのは度数が1番多い階級の階級値です。
したがって、度数分布表の最頻値は50点です。
ポイント
度数分布表の中央値
⇒中央のデータが属する階級の階級値
この度数分布表はデータが15個あります。
つまり、中央値はデータを大きさ順に並べたときの8番目のデータです。
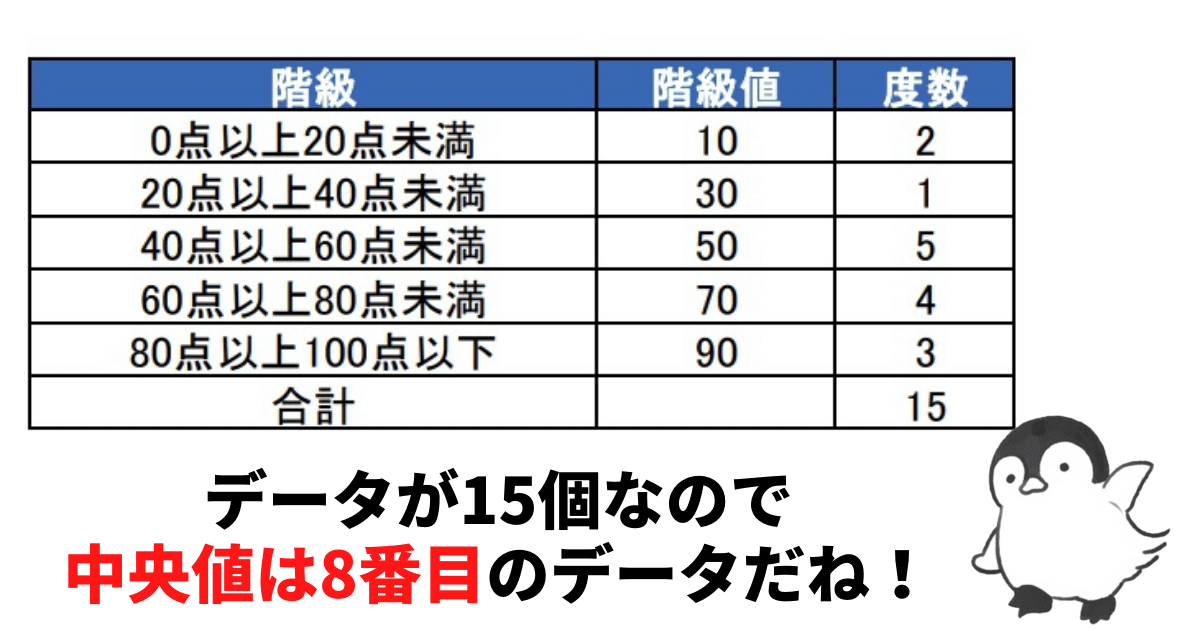
数えてみると8番目のデータが「40点以上60点未満」の階級に属していることが分かります。
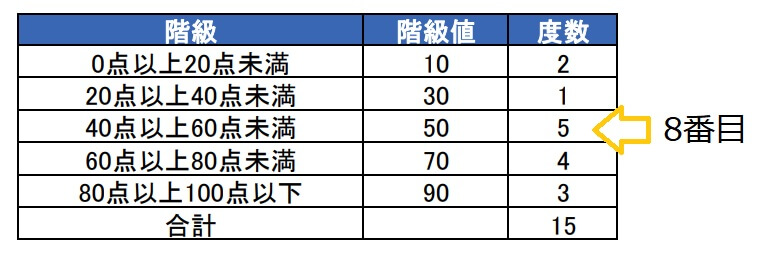
度数分布表の中央値は「中央のデータが属する階級の階級値」
したがって、中央値は50点となります。
度数分布表とヒストグラム
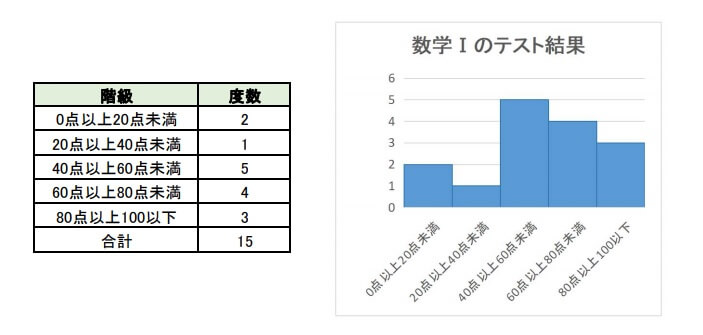
データの分布を区分けた表を度数分布表といい、それを棒グラフ状にしたものをヒストグラムといいます。


度数分布表からヒストグラムを書くこともあります。
ヒストグラムは度数分布表と合わせて覚えておきましょう。
-

ヒストグラムの書き方と平均値・中央値の求め方を解説!
続きを見る
累積度数
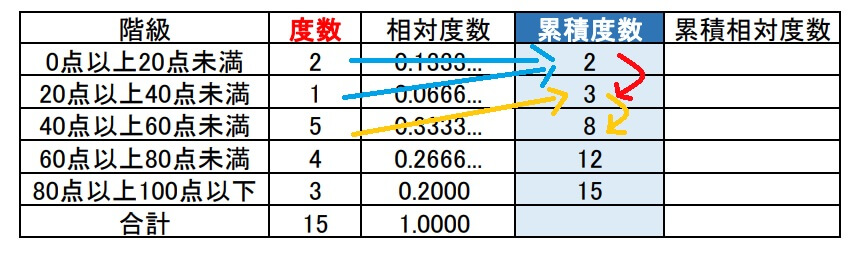
累積度数とは、その階級までの度数の合計です。
言葉で表現しきれなかったので、実際の度数分布表で確かめます。
累積度数は度数を足していきます。
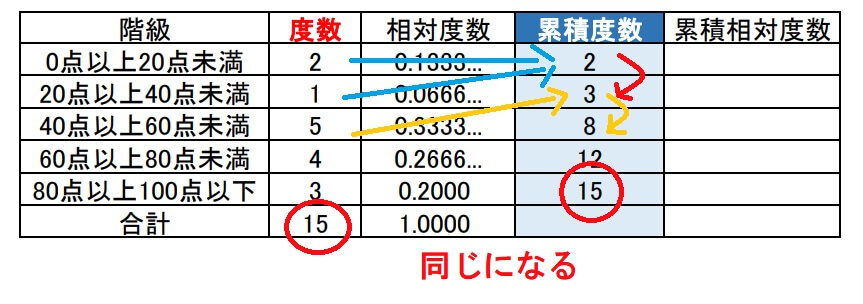
累積度数の最後の値は、度数の合計と必ず同じになります。
累積相対度数
累積相対度数も累積度数と同じ考え方で、その階級までの相対度数の合計を求めます。
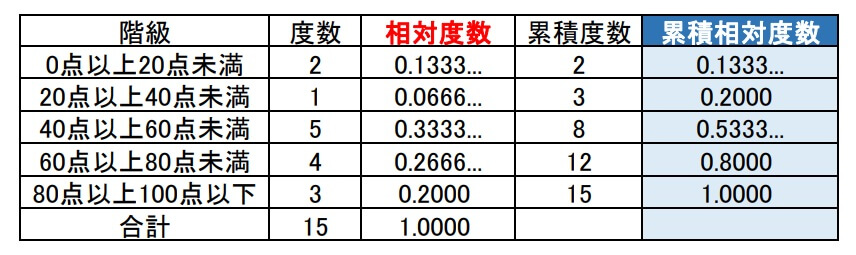
相対度数の値を順に足していきます。
順に加えていくと最後が1.000になりました。
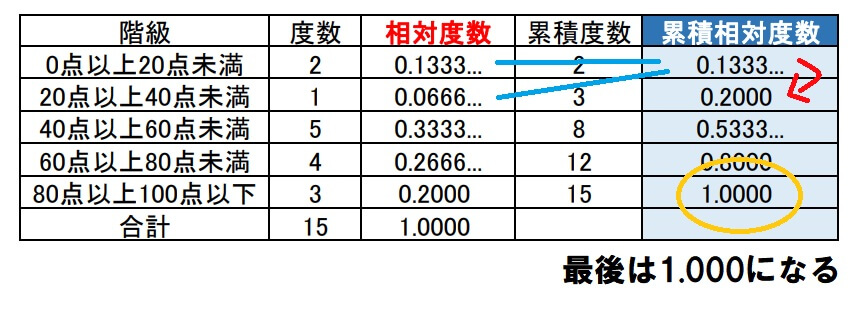
相対度数というのが、度数全体に対する割合を表していました。
したがって、累積相対度数の最後は必ず1.000になります。
度数分布表<練習問題>

ここまで度数分布表の用語の意味と各値の求め方を解説しました。
次は実際に度数分布表を埋める練習をしてみましょう。
下に高校1年生の数学Aのテストの結果があります。
このデータをもとに度数分布表を完成させてください。
28 36 19 64 35 7 73 79 51 44 66 47 95 35 26 (点)
【度数分布表】
| 階級 | 階級値 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 0以上20未満 | 10 | ア | 0.1333 | 0.1333 |
| 20以上40未満 | 30 | 5 | イ | ウ |
| 40以上60未満 | エ | 3 | 0.2000 | 0.6666 |
| 60以上80未満 | 70 | オ | 0.2667 | 0.9333 |
| 80以上100以下 | 90 | 1 | 0.0667 | 1.0000 |
| 合計 | - | 15 | 1.0000 | - |
度数分布表 まとめ
今回はデータの分析から度数分布表についてまとめました。
それぞれの言葉の意味と各値の求め方は覚えておきましょう。
度数分布表のポイント
度数分布表とは「データを階級ごとに分けたもの」

各値の求め方も確認しておきましょう。
各値の求め方
度数分布表の意味と各値の求め方が分かれば、すぐに得点アップにつながるのでこの機会にしっかり理解しておきましょう。
データの分析には重要な公式がたくさんあります。
分散や相関係数についても別記事でまとめているので合わせてご覧ください。
他にもデータの分析に関する悩みがある方は「データの分析まとめ記事」をご覧ください。
-

【数学Ⅰ】データの分析重要公式まとめ《完全攻略》
続きを見る
いまなら公式LINEから簡単なアンケートに答えるだけで、『データの分析』の重要公式をまとめたPDFをプレゼントしているので、ぜひ活用してください。









