「三角形の五心ってなに?」
「五心の性質を確認したい」
今回はこんな悩みを解決します。

三角形の五心とは、「重心」「内心」「外心」「垂心」「傍心」の5つの点を指します。

五心の中でもよく知られているものと、初めて聞くようなものもありますね。
本記事では三角形の五心それぞれの定義と性質をまとめました。
本記事を読めば三角形の五心について理解できるようにまとめましたので、ぜひ最後まで見ていってください。
本記事の見出し
三角形の五心

三角形の五心とは、「重心」「内心」「外心」「垂心」「傍心」の5つの点を指します。
5つの点は、それぞれ定義や性質がまったく異なります。
五心の定義
重心
"三角形の各頂点から引いた中線の交点"
①中線を2:1に内分する
②3:内部にできる6つの三角形は面積が等しい
内心
"三角形の内角の二等分線の交点"
①内接円の中心
②内心と各辺の距離が等しい
外心
"三角形の各辺の垂直二等分線の交点"
①外接円の中心
②外心と各頂点の距離が等しい
垂心
"各頂点から対辺に向かって引いた垂線の交点"
傍心
"角の二等分線と2つの外角の二等分線の交点"
五心はすべてコンパスと定規で作図できます。


三角形の五心 重心
三角形の重心について解説します。
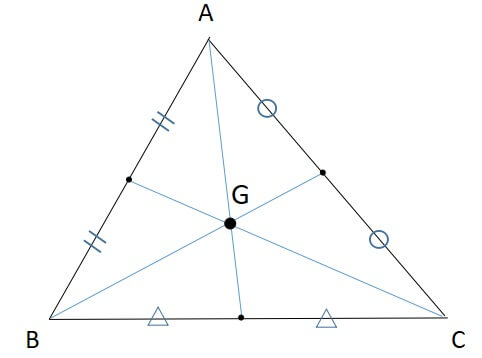
重心
重さの中心の点
英語で「center of Gravity」のため、点Gと表されることが多いです。
重心はスポーツなどでも聞く単語なので、比較的親しみやいですね。
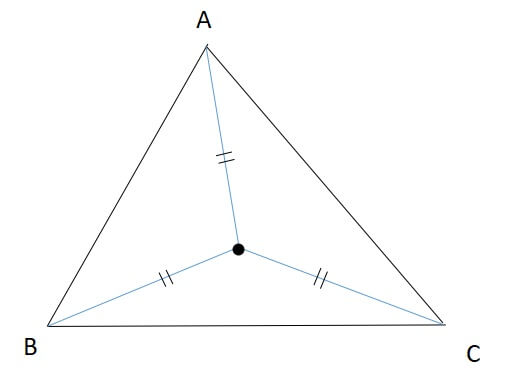
重心の定義は、「3本の中線の交点」です。
三角形の重心の定義
三角形の各頂点から引いた中線の交点
中線とは、頂点から向かい合う辺の中点を結んだ線を指します。

三角形の重心 性質
- 頂点と重心を結ぶと、向かい合う辺を二等分する
- 中線を2:1に内分する
1:頂点と重心を結ぶと、向かい合う辺を二等分する

三角形のある頂点から、重心を通るように直線を結ぶと向かい合う辺を二等分します。
これは重心の定義が、「3本の中線の交点」なので当然の性質です。
2:中線を2:1に内分する
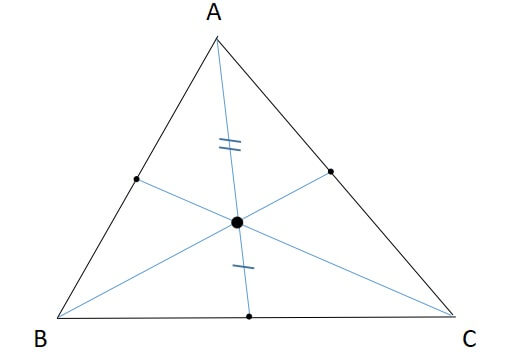
重心はそれぞれの中心を2:1になるように内分する性質があります。
この性質は中学校で習う、中点連結定理をつかって証明することができます。
重心についてもっと知りたい方は「三角形の重心とは?重心の性質と証明」をご覧ください。 続きを見る
三角形の重心の性質と証明!座標とベクトルの求め方も徹底解説!
三角形の五心 内心
三角形の内心について解説していきます。
内心は「内接円の中心」としてよく知られていますね。
三角形の内心の定義
三角形の内角の二等分線の交点
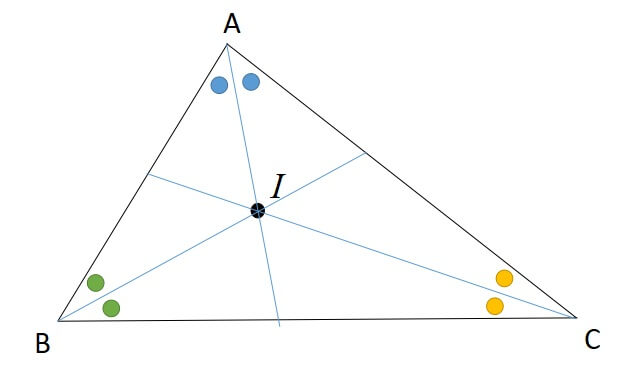
三角形の内心 性質
- 角を二等分する
- 内心と各辺との距離が等しい
- 内接円の中心
内心の性質と合わせて、内接円の性質も確認しておくと良いでしょう。
1:角を二等分する
定義が角の二等分線の交点なので、当たり前ですよね

2:内心と各辺との距離が等しい
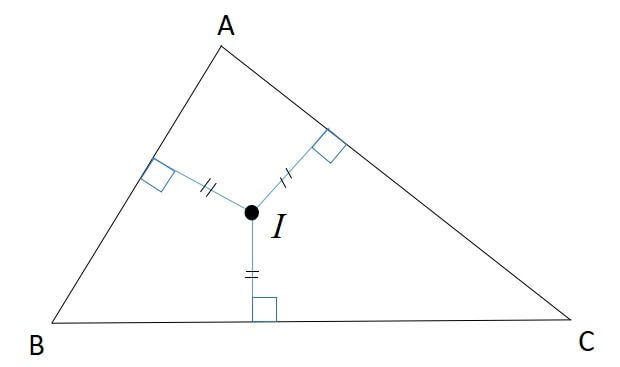
3:内接円の中心
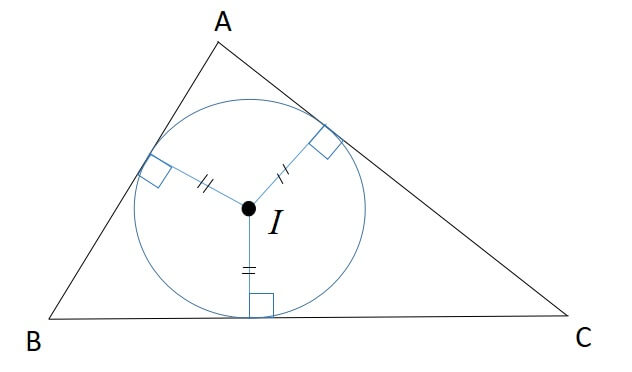
内心の性質の証明は「三角形の内心の性質と証明」にて解説しています。 続きを見る

三角形の内心とは?内心の意味や座標&ベクトルの求め方を解説
三角形の五心 外心
三角形の外心は油断すると忘れてしまいますよね。
外心は外接円の中心でもあるので要チェックです。
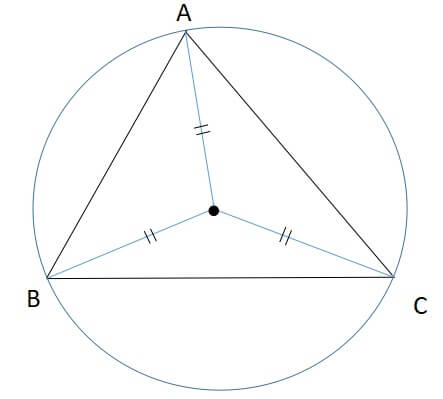
三角形の外心の定義
三角形の各辺の垂直二等分線の交点
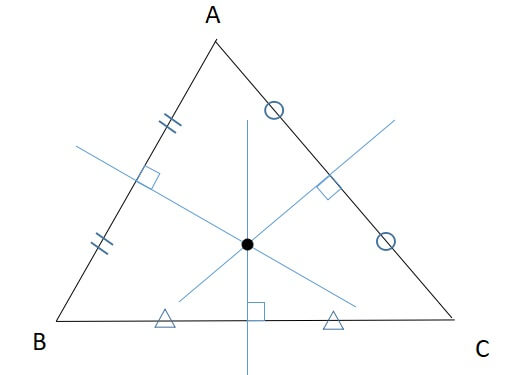
三角形の外心 性質
- 各辺に垂線を引くと二等分する
- 外心と各頂点との距離が等しい
- 外接円の中心
1:各辺に垂線を引くと二等分する

2:外心と各頂点との距離が等しい
3:外接円の中心
外心の性質の証明は「三角形の外心の性質と証明」にて解説しています。 続きを見る

三角形の外心の性質と証明
三角形の五心 垂心
三角形の垂心は名前の通り、垂線の集まる点です。
三角形の外心の定義
各頂点から対辺に引いた垂線の交点
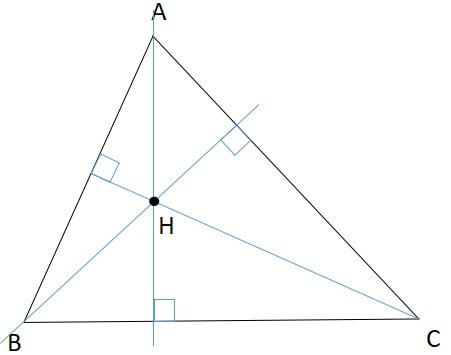
三角形の垂心 性質
- 四角形ADHF,BEHD,CFHEは円に内接する四角形である
- \(AH=2RcosA\)
1:四角形ADHF,BEHD,CFHEは円に内接する四角形である

2:\(AH=2RcosA\)
△ABCの外接円の半径をRとする。
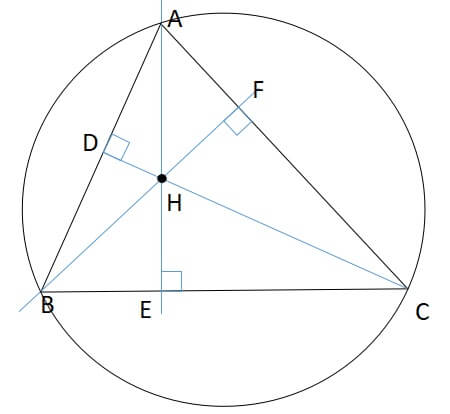
垂心の性質の証明は「三角形の垂心の性質と証明」にて解説しています。 続きを見る
三角形の垂心とは?垂心の性質と証明
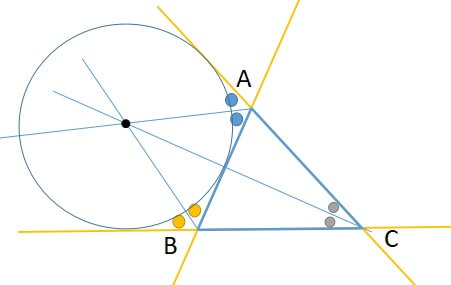
三角形の五心 傍心
おそらく「傍心」が三角形の五心のなかで1番マイナーだと思います。
知っておいて損はないので確認しておきましょう。
三角形の傍心の定義
角の二等分線と2つの外角の二等分線の交点
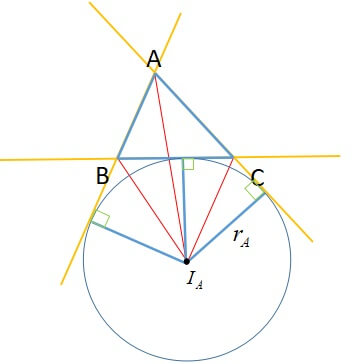
三角形の傍心 性質
三角形ABCの面積を\(S\)、\(\displaystyle s=\frac{a+b+c}{2}\)とすると、
\[S=\displaystyle \frac{1}{2} r_{A}(-a+b+c)=r_{A}(s-a)\]
三角形ABCの面積を\(S\)、\(s=\displaystyle \frac{a+b+c}{2}\)とすると、
\[S=\displaystyle \frac{1}{2} r_{A}(-a+b+c)=r_{A}(s-a)\]
傍心の性質の証明は「三角形の傍心とは?」にて解説しています。 続きを見る
三角形の傍心とは?傍心の性質と証明を解説!
五心すべての性質を覚えられるとベストですが、なかなか難しいと思います。
なので「内心」「重心」「外心」は五心の中でも重要なので優先して覚えてください。
図形に関するおすすめ勉強法

図形の問題はパターンがたくさんあります。
問題の意図をしっかり理解して、図形の性質を活用することが多いです。
次は図形に関する問題のおすすめ勉強法を紹介します。
- 教科書やノートを見直す
- 問題集で応用力を磨く
- 分かりやすい解説を見る
自分のいまの理解度と目標を照らし合わせて、自分に合った勉強法を試してみてください。

教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。
教科書には重要なポイントがギュッと詰まっています。

問題集で応用力を磨く

内心や重心の定義・性質を覚えたら問題を解いて応用力を磨きましょう。
- 教科書の例題
- 問題集の基本問題
- 問題集の応用問題
問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。
図形の学習におすすめの問題集を紹介します。
Amazon会員なら参考書も読み放題です。
初回30日間の無料体験あり。
⇒参考書が読み放題!Kindle Unlimitedについて詳しく知りたい
分かりやすい解説を見る
以下のような悩みがあるなら映像授業もおすすめです。
- 勉強しても成績が伸びない
- 学校の授業が分かりにくい
- 分からない所が分からない
映像授業なら自分に必要な授業のみを受けられるうえに、分かるまで繰り返し視聴することができます。
分からないを1つずつ解消していけるので、定期テストで高得点を取りたい方は授業授業がおすすめです。
映像授業で学ぶメリット

映像授業で学ぶことのメリットを3つ紹介します。
映像授業で学ぶメリット
- 勉強に対する苦手意識がなくなる
- 目標に最短ルートで近づける
- 楽しい高校生活と勉強の両立
勉強に対する苦手意識がなくなる

映像授業では各教科のプロが授業をするので、かなり分かりやすい解説が多いです。
高校生のつまづきやすいポイントをしっかりと押さえた分かりやすい授業で、苦手単元を1つずつ解消していきます。
目標に最短ルートで近づける
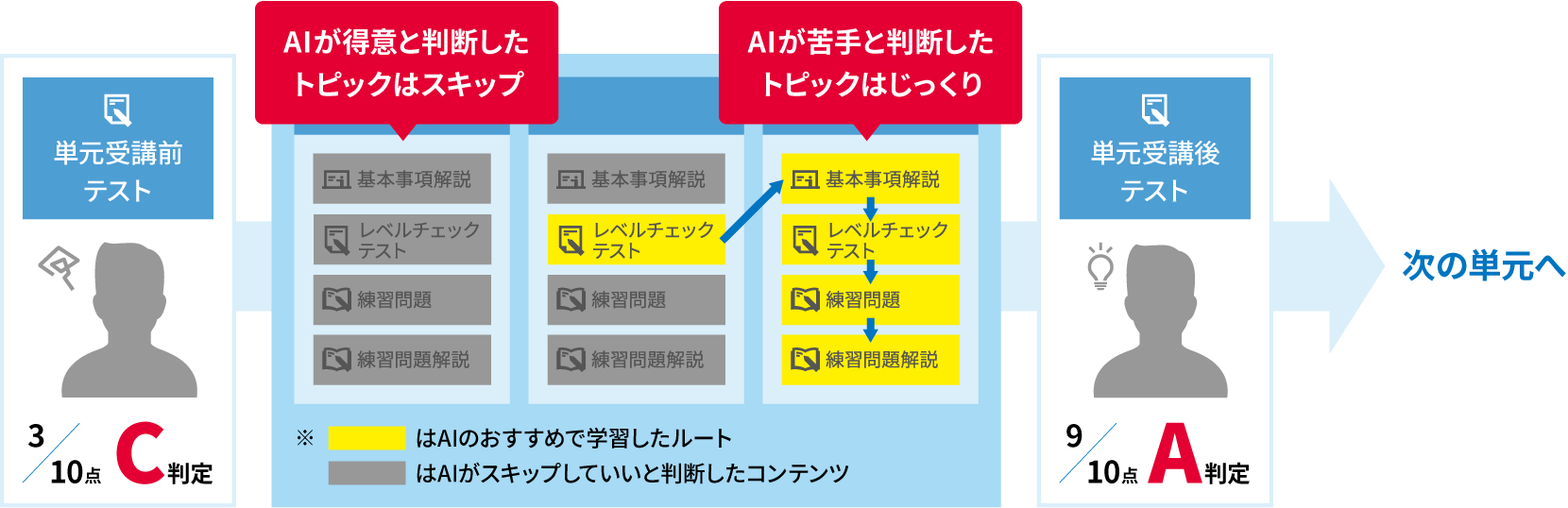
河合塾Oneの「自分専用カリキュラム」
自分に必要な授業だけを受けられるので、最短ルートで目標に近づきます。
ただひたすらに解説を写すような勉強は時間がもったいないです。
自分のレベルに合わせた授業だけを受けて、最短で目標達成を目指します。
楽しい高校生活と勉強の両立

1回の授業が15分程度で、ネット環境があればどこからでも受講できます。
通学の電車でもサクッと復習できるので、部活や遊びとの両立も可能です。
目的に合わせて選ぶことが重要

映像授業といっても様々なサービスがあります。
どこでも良いわけではなく、あなたの目標に合った映像授業を選ぶことが重要です。
| サービス名 | こんな方におすすめ |
| 河合塾One | 定期テスト対策がしたい |
| スタディサプリ | 受験に向けて勉強したい |
| 進研ゼミ | テキストも欲しい |
"河合塾One"と"スタディサプリ"には無料体験があります。
どちらも会員数をグングン伸ばしているので、いつ無料体験がなくなるか分かりません。
ちなみに、定期テスト対策なら「河合塾One」、受験に向けて始めるなら「スタディサプリ」がおすすめです。
無料体験期間
定期テストに向けて無料体験の期間で総復習するのもオススメです!
高校生向けの映像授業をランキング形式でまとめました。


三角形の五心 まとめ
今回は三角形の五心についてまとめました。
点の性質の証明については、それぞれ記事にしているので、ぜひご覧ください。
各点の記事
五心が問題になるときは、それぞれの性質を知っている前提で出題されることが多いです。
ここで紹介した性質だけで十分なので、必ず確認しましょう。
五心以外の図形の単元についても記事を出しています。
-

チェバの定理の使い方や証明を解説!簡単に辺の長さが求められる!
続きを見る
-

メネラウスの定理とは?公式の覚え方と使い方を解説!
続きを見る
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。








