今回解決する悩み
「弧度法ってなに?」
「度数法から弧度法に変換したい」

数Ⅱの三角関数では円の中心角を\(180^\circ\)や\(360^\circ\)といった度数法ではなく、\(\pi\),\(2\pi\)など弧度法で表します。
慣れるまでは難しく思えるかもしれません。
ぼくも始めはよく分からず使っていたので大丈夫です。
三角関数では弧度法を用いることが主流なので意味はしっかり押さえておきましょう。
本記事では弧度法の意味および度数法から弧度法への変換方法について解説していきます。
※本ページは学習アプリのプロモーションが含まれています。

ぜひ最後までご覧ください。
弧度法とは?

弧度法というのは、名前の通り”弧”に注目して角度を表現する方法のことです。
円の半径と弧の長さが等しくなる角度を1rad(ラジアン)といいます。
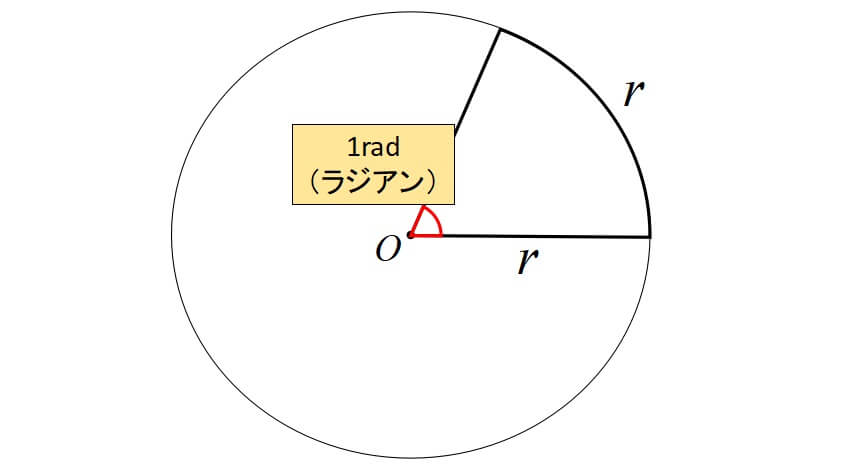
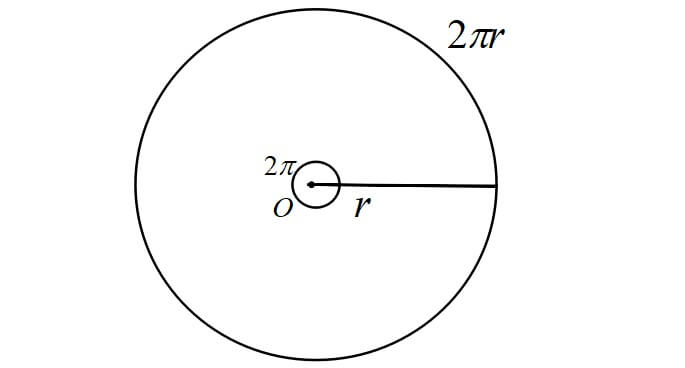
半径\(r\)の円において、円周の長さは\(2\pi r\)となり、この時の中心角を\(2\pi\)ラジアンといいます。
半円の場合は、円周の長さが\(\pi r\)なので、中心角は\(\pi\)ラジアンです。
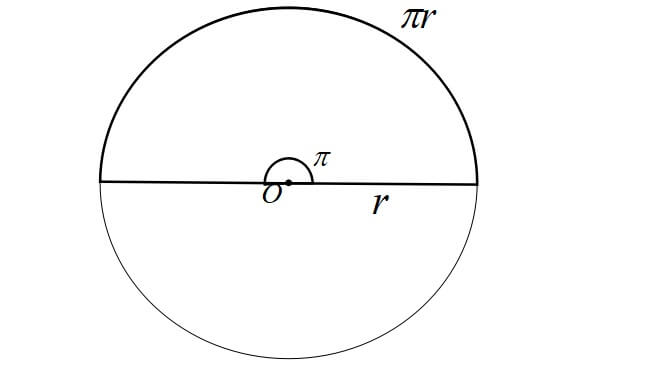
つまり、\(360^\circ=2\pi\),\(180^\circ=\pi\)です。
他の角度も弧度法に直したので確認してみてください。

弧度法と度数法の変換
弧度法を度数法に変換したり、逆に度数法から弧度法に変換したりできるようにしましょう。
ポイントは\(\pi=180^\circ\)であることです。
度数法から弧度法へ変換
まずは度数法から弧度法に直していきましょう。
\(180^\circ=\pi\)なので、
\(180^\circ\)を\(\pi\)に置き換えます。
つまり、\(180^\circ\)で割って\(\pi\)を掛けたら変換完成です。
\begin{eqnarray}
90^\circ &=& 90^\circ \div 180^\circ \times{\pi}\\
\displaystyle &=& 90^\circ \times \frac{\pi}{180^\circ}\\
\displaystyle &=& \frac{\pi}{2}
\end{eqnarray}
これで変換完成です。
練習問題を最後の章で用意しているので、ぜひ解いてみてください!
弧度法から度数法へ変換
次は弧度法から度数法へ変換します。
\(\pi=180^\circ\)なので、
\(\pi\)を\(180^\circ\)に置き換えます。
つまり、\(\pi\)に\(180^\circ\)を代入します。
\begin{eqnarray}
\displaystyle\frac{\pi}{3} &=& \frac{180^\circ}{3}\\
&=& 60^\circ
\end{eqnarray}
これで変換完成です。
こちらも練習問題を最後の章で用意しているので、ぜひ解いてみてください!
弧度法を使うメリット

なぜわざわざ弧度法を使うのか、弧度法のメリットを紹介します。
・弧度法のメリット1つ目は、弧の長さ,面積が簡単に求められます。
次の章「扇形の弧の長さと面積の公式」で解説するから分かるように、弧度法も用いると簡単に扇形の弧の長さと面積が求められるようになります。
弧の長さと面積の公式
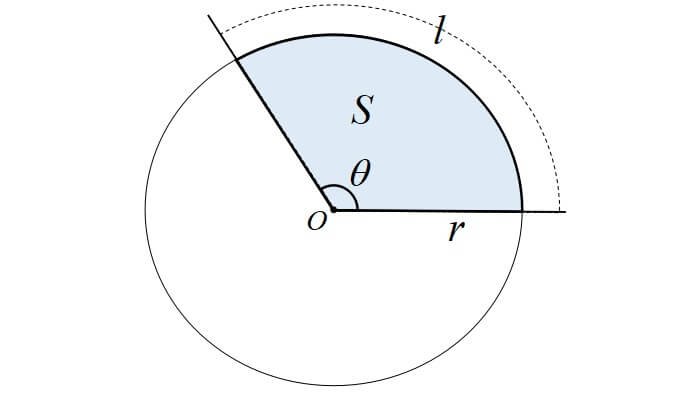
半径 \(r\),中心角 \(\theta[\mathrm{rad}]\) の原形の弧の長さを\(l\),面積を\(S\)とすると
弧の長さ\(l\) \(l=r \theta\)
面積\(S\) \(\displaystyle S=\frac{1}{2} r^{2} \theta=\frac{1}{2} r l\)
扇形の弧の長さと面積の公式

弧の長さと面積の公式
半径 \(r\),中心角 \(\theta[\mathrm{rad}]\) の原形の弧の長さを\(l\),面積を\(S\)とすると
弧の長さ\(l\) \(l=r \theta\)
面積\(S\) \(\displaystyle S=\frac{1}{2} r^{2} \theta=\frac{1}{2} r l\)
つまり、扇形の弧の長さは(半径)×(中心角)で求められます。
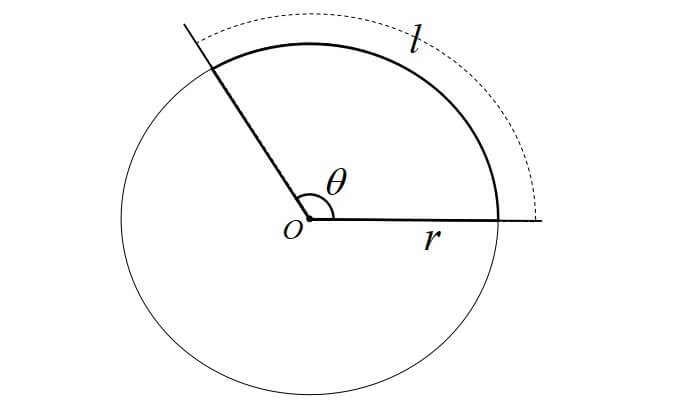
また、扇形の面積は\(\displaystyle \frac{1}{2}\)×\((半径)^2\)
もしくは\(\displaystyle \frac{1}{2}\)×(半径)×(弧の長さ)で求めることができます。
弧の長さと面積の公式 <証明>
弧の長さと面積の公式の証明をしておきます。
証明が必要ない方は、次の章へ進んでください。
【扇形の弧の長さ】
扇形の弧の長さは中心角の大きさに比例する。
中心角が2倍になれば、弧の長さも2倍になる。
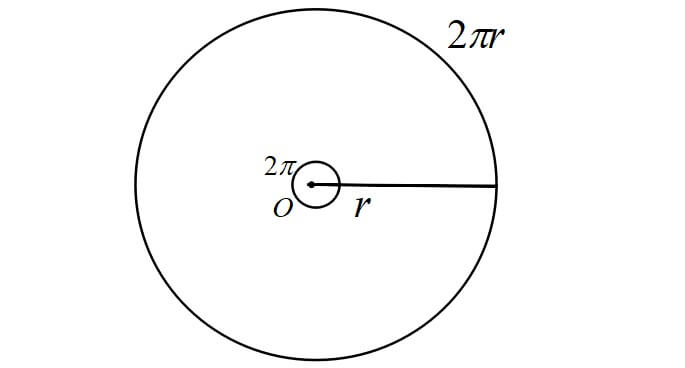
半径\(r\)の円周は\(2\pi r\),中心角は\(2\pi\)だから比例式は
\[l:2\pi r=\theta:2\pi\]
これを計算すると、
\[2l\pi=2\pi r \theta\]
よって、\(l=r \theta\)となり証明終了です。
【扇形の面積】
面積も弧の長さと同様に比例式を使います。
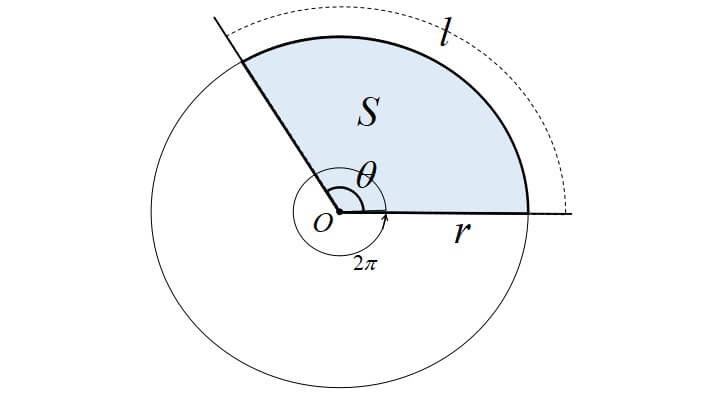
扇形の面積も中心角の大きさに比例するので,半径\(r\)の円の面積は\(\pi r^{2}\),中心角\(2\pi\)なので
比例式 \(S:\pi r^{2}=\theta:2\pi\)
これを計算して、
\[2\pi S=\pi r^{2} \theta\]
\[\displaystyle S=\frac{1}{2} r^{2} \theta\]
\(l=r \theta\)なので
\[\displaystyle S=\frac{1}{2} r l\]
となり、証明終了です。
弧度法<練習問題>

問1.\(90^\circ\)
問2.\(45^\circ\)
問3.\(240^\circ\)
解答
度数法から弧度法に直すときは、「\(180^\circ\)で割って\(\pi\)を掛ける」だったので、
《問題①》
\begin{eqnarray}
90^\circ &=& 90^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{\pi}{2}
\end{eqnarray}
《問題②》
\begin{eqnarray}
45^\circ &=& 45^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{\pi}{4}
\end{eqnarray}
《問題③》
\begin{eqnarray}
240^\circ &=& 240^\circ \div{180^\circ}\times{\pi}\\
&=& \displaystyle \frac{4}{3} \pi
\end{eqnarray}
問1.\(\displaystyle \frac{\pi}{4}\)
問2.\(\displaystyle \frac{2}{3} \pi\)
問3.\(\displaystyle \frac{11}{6} \pi\)
解答
弧度法から度数法へ変換する場合は、\(\pi\)に\(180^\circ\)を代入しましたね!
《問題①》
\begin{eqnarray}
\displaystyle \frac{\pi}{4} &=& \frac{180^\circ}{4}\\
&=& 45^\circ
\end{eqnarray}
《問題②》
\begin{eqnarray}
\displaystyle \frac{2}{3} \pi &=& \frac{2}{3} \times{180^\circ}\\
&=& 120^\circ
\end{eqnarray}
《問題③》
\begin{eqnarray}
\displaystyle \frac{11}{6} \pi &=& \frac{11}{6} \times{180^\circ}\\
&=& 330^\circ
\end{eqnarray}
弧度法まとめ
今回は数学Ⅱの三角関数から弧度法の意味についてまとめました。
\(180^\circ\)が\(\pi\)に置き換わっただけなので、難しく考えないほうが良いでしょう。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!
マストラ公式LINEアカウントを友達登録しよう!
マストラのLINE公式アカウントができました!

~実際の公式LINEのメニュー~
LINE画面からワンタップで各単元のまとめ記事が読めるようになるよ!
高校生向けの様々なコンテンツを配信予定!
勉強に関する相談や質問にも答えるので、気軽にメッセージを送ってね!
▼この機会にぜひ登録!
完全個別指導のスタディトレーナー

スタディトレーナーは高校生の勉強を支える学習コーチングサービスです。
学習塾やオンライン家庭教師とは違い、365日いつでも質問や相談ができます。
目標に合わせた学習計画で、あなたの志望校合格を実現させます。
スタディトレーナーが行う
7つのサポート
- 完全個別指導で苦手を克服!
- 勉強のやり方から教えるので安心!
- 目標から逆算した学習計画の作成
- 1人ひとりに合った参考書をお届け
- 映像授業で予習復習もバッチリ
- 24時間365日LINEで質問可能
- 進路相談もいつでも対応!
無料体験授業から始められるので、お気軽に申し込み下さい。






